2. Методы анализа и синтенза САУ
Основными требованиями, предъявляемыми к системе автоматического управления, являются: устойчивость, точность отработки задающего воздействия, нечувствительность к мешающим воздействиям и качество переходного процесса. Указанные требования выражаются через числовые характеристики, называемые показателями качества САУ.
Для определения показателей качества САУ используются прямые и косвенные методы анализа качества.
Прямыми называются методы, позволяющие судить о качестве на основе анализа реакции САУ на внешнее воздействие путем решения дифференциального уравнения САУ, а также нахождения интеграла свертки. Существует два основных способа решения дифференциальных уравнений с постоянными коэффициентами: классический способ и операторный, основанный на преобразовании Лапласа. На практике прямые методы применяют для анализа качества САУ, описываемых уравнениями динамики не выше 2…3 порядка.
Косвенными называются методы, позволяющие судить о качестве без определения реакции САУ на внешнее воздействие. Из косвенных методов наибольшее распространение получили метод коэффициентов ошибок, частотный метод и метод интегральных оценок.
Достоинством косвенных методов по сравнению с прямыми является простота их применения и возможность сравнительно простой оценки влияния параметров системы на ее качество.
Основной недостаток косвенных методов заключается в том, что они дают приближенные оценки показателей качества переходного и установившегося режимов.
2.1.1. Понятие устойчивости. Анализ устойчивости САУ
Любая система автоматического управления прежде всего должна быть работоспособной, то есть обеспечивать поставленную цель управления. Так, в следящей системе выходной процесс должен как можно точнее повторить задающее воздействие х(t). Любое реальное воздействие, конечно, ограниченно по амплитуде, поэтому в работоспособной системе выходной процесс также ограничен. Если выходной процесс с течением времени неограниченно возрастает, то система называется неустойчивой, то есть неработоспособной.
Изучением условий, при которых система будет работоспособной, занимается теория устойчивости. На рис. 43, а показаны процессы в устойчивой следящей системе, а на рис.43, б – неустойчивой.
Рис. 43. Процессы в устойчивой (а) и неустойчивой (б) системах
Одной из особенностей линейных систем (как стационарных, так и нестационарных) является то, что условия устойчивости в них не зависят от воздействий. Так, например, если система устойчива при воздействии типа единичной функции, то можно утверждать, что она будет работоспособной и при любом другом воздействии.
Выходной процесс в стационарной системе состоит из двух слагаемых
y(t) = yв(t) + yn(t),
где yв(t) – вынужденный процесс, определяемый задающим воздействием x(t), yn(t) – переходный процесс за счет ненулевых начальных условий. В устойчивой системе переходный процесс с течением времени стремится к нулю, т.к. он не имеет информации о задающем воздействии x(t).
Так как характер воздействия не
влияет на условия устойчивости, то их удобно оценивать по переходному процессу
yп(t). В устойчивой системе с течением времени
при 
что
называется асимптотической устойчивостью, а в неустойчивой системе 
.
Задача теории устойчивости состоит в разработке методики, позволяющей по уравнению и передаточной функции системы определять условия устойчивости.
2.1.2. Алгебраический критерий устойчивости
Для определения устойчивости необходимо составить характеристическое уравнение D(p) и найти его корни. Составить его можно, воспользовавшись передаточной функцией САУ.
Для устойчивости линейной стационарной системы автоматического управления необходимо и достаточно, чтобы вещественные части всех корней характеристического уравнения системы были отрицательными. Если, корни расположить на комплексной плоскости (рис.44), то геометрическая интерпретация необходимых и достаточных условий устойчивости будет следующей: система устойчива, когда все корни характеристического уравнения располагаются в левой полуплоскости комплексной плоскости корней.
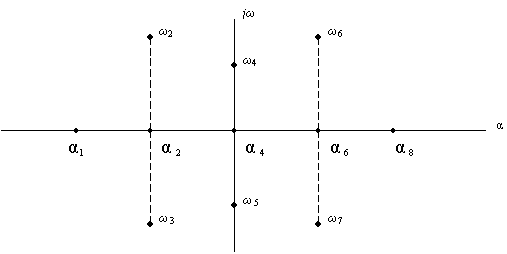
Рис. 44. Комплексная плоскость корней
Если хотя бы один корень находится в правой полуплоскости, то система неустойчива. Если корни располагаются на мнимой оси, то система находится на границе устойчивости и переходной процесс будет иметь постоянную амплитуду.
Общий вид характеристического уравнения
D(p) = C0 + C1(p) + … + CnPn,
где C0, C1 … Cn – коэффициенты, Pi – корни характеристического уравнения.
Например: Pi = a i, Pk = a k + jw k, Pk+1 = a k - jw k.
Полином D(p) является знаменателем передаточной функции.
Непосредственное нахождение корней характеристического уравнения доступно лишь для уравнений первого и второго порядка. При n > 2 решение или громоздко, или вообще в аналитической форме невозможно. В связи с этим возникает задача суждения об устойчивости косвенными методами, позволяющими оценить расположение корней характеристического уравнения на комплексной плоскости без непосредственного их определения. Решают ее с помощью определенных правил, называемых критериями устойчивости.
Рассмотрим вариант алгебраического критерия устойчивости, доказанного немецким ученым Гурвицем в 1895 году.
Система будем устойчивой, если все коэффициенты C > 0 и одновременно выполняются неравенства, зависящие от коэффициентов C и порядка системы n. Для систем первого и второго порядков условия устойчивости соответствуют положительным значениям коэффициентов. При n > 4 выражение для условий устойчивости становится громоздким.
Пример. Пусть в следящей системе передаточная функция в разомкнутом состоянии,
имеет вид:
Необходимо
определить, при каком соотношении параметров системы
K, T1, T2 и T3 замкнутая система будет устойчивой. Для решения этой задачи запишем характеристическое уравнение замкнутой системы.
D(p) = P(p) + Q(p) = K + p (1+KT2) + p2 (T1+T2) + p3T3T1 = 0.
Для n = 3 получаем следующие условия устойчивости:
(T3 +T1) (1 +KT2) - KT1T3 > 0 или K[T1T3 – T2 (T1+T3)] < T1 + T3.
Отсюда имеем неравенства:
Если в полученных выражениях знак неравенства заменить, то можно построить линию границы устойчивости в плоскости параметров системы.
На рис. 45 для примера показана область устойчивости исследуемой системы в плоскости K и T2.
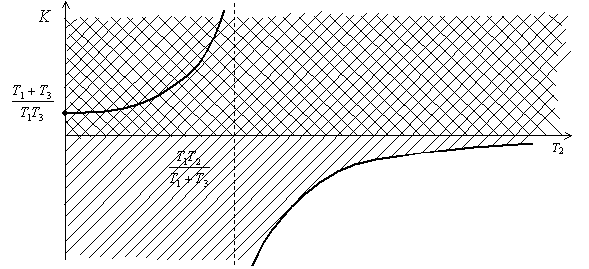
Рис. 45. Область устойчивости
Так как параметры системы неотрицательны, то практически область устойчивости соответствует части области показанной двойной штриховой.
Приведенный пример иллюстрирует одно из достоинств критерия Гурвица – возможность в аналитической форме связать условия устойчивости с параметрами системы и, следовательно, построить области устойчивости в плоскости этих параметров. К сожалению, подобная задача сравнительно легко решается при малых порядках характеристического уравнения. Кроме того, критерий не позволяет оценить местоположение корней на комплексной плоскости, что имеет большое значение для определения свойств системы. И наконец, критерием нельзя воспользоваться, когда нет аналитического выражения для характеристического уравнения, что делает невозможным непосредственное применение экспериментальных данных.
2.1.3. Частотный критерий устойчивости
Наиболее широкое практическое применение для исследования устойчивости систем с обратной связью получил критерий, основанный на рассмотрении частотных характеристик разомкнутых САУ. Этот критерий был предложен в 1932 г. американским ученым Найквистом для расчетов усилителей с обратной связью и носит его имя. Впервые в теорию автоматического управления он был введен советским ученым А.В.Михайловым в 1936 г.
Основные достоинства частотного критерия, обусловившие его широкое распространение:
1. Критерий применим в тех случаях, когда дифференциальные уравнения системы или отдельных ее звеньев неизвестны, но известны частотные характеристики, полученные, например, экспериментально.
2. Использование критерия не так резко усложняется при увеличении порядка характеристического уравнения, как это имеет место при применении алгебраического критерия.
3. Критерий Найквиста еще в большей степени, чем критерий Гурвица, позволяет непосредственно установить влияние на устойчивость системы различных ее звеньев.
4. Критерий дает представление о степени устойчивости системы и показывает возможные пути ее улучшения, если в этом есть необходимость.
5. Критерий позволяет связать исследование устойчивости с последующим анализом качества как в установившемся, так и в переходном режимах.
Частотный критерий Найквиста связывает устойчивость замкнутой САУ с ходом АФХ разомкнутой системы.
АФХ изображается на комплексной плоскости. Для этого комплексная функция K (jw ) представляется в виде ее действительной и мнимой частей.
K(jw ) = ReK(jw ) + jI mK(jw ).
Значения ReK(jw
) и ImK(jw ) откладываются вдоль координатных осей и
функция K(jw ) изображается в виде вектора. При изменении
w от 0 до 
конец вектора описывает на плоскости некоторую кривую (годограф), которая и
является АФХ (рис.46)
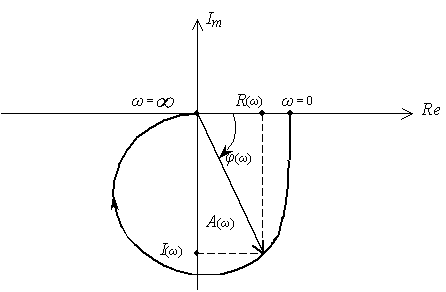
Рис.46. АФХ разомкнутой следящей системы
Критерий Найквиста позволяет судить об устойчивости замкнутой САУ в случаях устойчивой и неустойчивой исходной разомкнутой системы.
Критерий Найквиста для случая,
когда разомкнутая система устойчива, формулируется следующим образом: замкнутая
система будет устойчивой, если при изменении частоты w от 0 до
АФХ устойчивой разомкнутой системы не охватывает точку с координатами - 1,
j0.
Для иллюстрации критерия на рис. 47 показаны АФХ устойчивой (а) и неустойчивой (б) систем в разомкнутом состоянии.
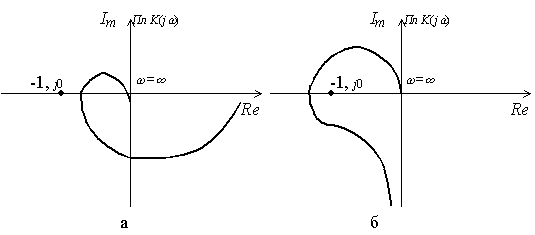
Рис.47. АФХ устойчивой (а) и неустойчивой (б) систем
Таким образом частотный критерий Найквиста позволяет судить об устойчивости замкнутой САУ по виду АФХ исходной разомкнутой САУ (устойчивой или неустойчивой).
2.1.4. Логарифмический критерий устойчивости. Запасы устойчивости.
Рассмотрим типовую САУ с единичной обратной связью (рис.48).
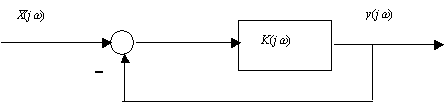
Рис.48. Структурная схема типовой САУ с единичной обратной связью
При подаче на вход САУ воздействия вида комплексная гармоническая функция
реакция системы будет также комплексной гармонической функцией
.
Предположим, что при частоте w / комплексная передаточная функция разомкнутой системы K(jw /) = -1.
Тогда
т.е. система становится неустойчивой.
Условие K(jw ’) = -1, при котором система теряет устойчивость, может быть записано в виде совокупности условий для амплитудной и фазовой частотных характеристик
Условие (27) получило название условия баланса амплитуд, условие (28) - баланса фаз.
Физически сущность потери устойчивости состоит в том, что входной сигнал передается системой на выход без ослабления, т.к. A(w ) = 1, но с противоположным знаком, т.к. /Y (w )/ = 180° . По цепи обратной связи сигнал y(t) = - x(t) вновь поступает на вход системы с тем же знаком и с той же амплитудой, что и исходный сигнал. В результате ошибка становится равной
E(t) = x(t) - y(t) = 2x(t),
выходной сигнал нарастает, вновь складывается со входным и т.д. до бесконечности.
Рассуждая аналогично, можно показать, что система будет устойчива тогда, когда при выполнении одного из условий - баланса амплитуд или баланса фаз - другое условие нарушается в меньшую сторону, т.е. если
а) при A (w c) = 1 или L(w c) = 0:
/Y (w c)/ < 180° ;
б) при /Y (w
)/ = 180° , A (w)
< 1 или
L (w)
< 0.
Здесь w c - частота среза разомкнутой САУ, когда A(w c) = 1, w p - частота, на которой ФЧХ пересекает линию - 180° .
Строгое доказательство частотных критериев устойчивости замкнутых систем было выполнено в 30-х годах советским ученым А.В.Михайловым и американским ученым Г.Найквистом. Наибольшее практическое применение получил критерий, позволяющий оценивать устойчивость замкнутой САУ по логарифмическим частотным характеристикам разомкнутой САУ:
для устойчивости замкнутой САУ при устойчивой разомкнутой САУ необходимо и достаточно, чтобы на интервале частот от w = 0 до w = w c фазочастотная характеристика разомкнутой САУ не пересекала (или пересекала четное число раз) линию - 180° .
Пример.
Передаточная функция разомкнутой САУ
Определить устойчивость САУ по виду частотных характеристик.
Логарифмические частотные характеристики этой системы представлены на рис.49.
Рис.49. Логарифмические амплитудно-частотная и фазочастотная характеристики
На участке 0 ... w c ФЧХ пересекает линию - 180° один раз. При этом на частоте среза /Y (w c)/ > 180° . Следовательно, система неустойчива. Этот же вывод следует из критерия Гурвица, согласно которому предельное значение коэффициента усиления равно
.
Таким образом, для того, чтобы система была работоспособной, нужно или уменьшать ее коэффициент усиления до Kv < Kv пред, или принимать специальные меры - корректировать систему.
При уменьшении коэффициента усиления вид частотных характеристик системы не изменяется, а ЛАЧХ опускается параллельно оси L(w ) вниз.
ЛАЧХ должна быть опущена до такого
уровня, когда окажется, что wc < w
.. Этот признак также является условием устойчивости САУ.
2.1.5. Запасы устойчивости САУ по амплитуде и по фазе
В процессе эксплуатации САУ ее параметры изменяются, что приводит к искажению вида амплитудных и фазовых частотных характеристик системы. В результате ранее устойчивая система может стать неустойчивой.
Для оценки возможных пределов деформации амплитудной и фазовой частотных характеристик используют специальные параметры - запасы устойчивости по усилению и по фазе.
Запасом устойчивости по усилению называется число, показывающее, во сколько раз коэффициент усиления разомкнутой САУ меньше предельного.
,
или
.
Запас устойчивости по усилению
характеризует возможные пределы деформации амплитудной частотной характеристики
САУ, при которых она окажется на грани устойчивости. Запас устойчивости по усилению
может быть определен не только путем расчета по приведенной ранее формуле, но
и из логарифмических частотных характеристик. Действительно, для того, чтобы
система оказалась на грани устойчивости, необходимо выполнение одновременно
с условием баланса фаз Y (w)
= - 180° также и условия баланса амплитуд, т.е. необходимо, чтобы
A(w p ) = 1
= Kпред (w).
Тогда
или
.
Таким образом, запас по усилению
равен значению ЛАЧХ разомкнутой САУ на частоте w,
взятому с обратным знаком.
Запасом устойчивости по фазе называется значение фазового сдвига, недостающего до выполнения условия баланса фаз на частоте среза w с разомкнутой САУ:
.
Таким образом, запас по фазе характеризует возможные пределы деформации ФЧХ системы, при которых она окажется на грани устойчивости, если выполняется условие баланса амплитуд: А(w с) = 1, или L(w ) = 0. На графиках логарифмических частотных характеристик запас по фазе определяется как величина фазового сдвига между линией (-180° ) и ФЧХ на частоте среза.
Отметим, что запас по усилению в литературе часто неточно называется запасом по амплитуде.
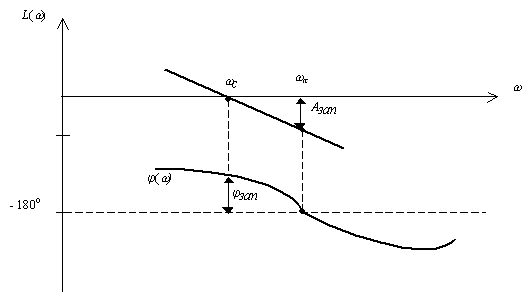
Рис.50. Логарифмические характеристики
Таким образом Азап характеризует возможные пределы деформации АЧХ системы, а Y зап - возможные пределы деформации ФЧХ системы, при которых она окажется на грани устойчивости.
Предыдущий
пункт | Наверх | Следующий пункт
| Оглавление |