1.5. Основные характеристики типовых звеньев и САУ
1.5.1. Временные характеристики
Связь между выходным процессом и входными воздействиями во временной области записывается посредством временных характеристик.
Временной характеристикой
называется реакция системы на типовое воздействие при нулевых начальных условиях.
В качестве типовых воздействий используют единичный импульс и единичную функцию.
На рис. 23. изображен прямоугольный импульс малой длительности
![]() с амплитудой 1\
с амплитудой 1\![]() .
.

Рис. 23. Единичный импульс
Очевидно, что площадь такого импульса
равна единице. Устремляя ![]()
![]() 0, в пределе будем иметь единичный импульс или дельта-функцию
0, в пределе будем иметь единичный импульс или дельта-функцию ![]() (t).
Она обладает следующими свойствами:
(t).
Она обладает следующими свойствами:
|
|
(11) |
Реакция системы на единичный импульс
при нулевых начальных условиях называется импульсной характеристикой
kyx(t). Так как свойства стационарной системы с течением
времени не меняются, то единичный импульс ![]() (t-
(t-![]() ),
приложенный в момент времени t =
),
приложенный в момент времени t = ![]() ,
вызовет реакцию kyx(t-
,
вызовет реакцию kyx(t- ![]() ),
аналогичную по форме, но сдвинутую по времени на интервал
),
аналогичную по форме, но сдвинутую по времени на интервал ![]() (рис. 24).
(рис. 24).
Вследствие того, что система линейная,
реакция на импульс ad (t - ![]() )
будет равна akyx(t -
)
будет равна akyx(t - ![]() ),
где а произвольная постоянная. Импульсная характеристика равна нулю до
момента приложения воздействия
),
где а произвольная постоянная. Импульсная характеристика равна нулю до
момента приложения воздействия
|
kyx(t - t ) = 0 при t < t . |
(12) |
Это равенство называется условием физической реализуемости. Покажем, как посредством импульсной характеристики определяется выходной процесс при произвольном воздействии.
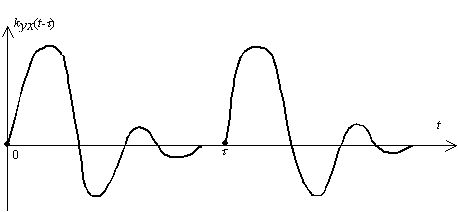
Рис. 24. Импульсная характеристика
Пусть воздействие x(t)
является некоторой функцией, показанной на рис. 25. Представим
x(t) в виде суммы прямоугольных импульсов малой длительности ![]()
![]() ,
следующих вплотную друг за другом.
,
следующих вплотную друг за другом.
Получающаяся при этом ступенчатая
функция будет стремиться к точной функции x(t), если устремить
![]()
![]()
![]() 0.
При достаточно малой величине
0.
При достаточно малой величине ![]()
![]() каждый из импульсов может приближенно рассматриваться как дельта-функция с площадью
x(t i)
каждый из импульсов может приближенно рассматриваться как дельта-функция с площадью
x(t i)![]()
![]() . Реакция системы на этот импульс в момент t будет приблизительно равна
x(
. Реакция системы на этот импульс в момент t будет приблизительно равна
x(![]() i)kyx(t
-
i)kyx(t
- ![]() i)
i)![]()
![]() ,
что показано на рис. 25.
,
что показано на рис. 25.
Реакция от всех импульсов, лежащих в интервале от 0 до t, будет равна сумме реакций от каждого из импульсов в отдельности, то есть
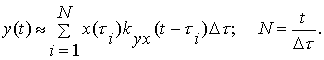
Переходя к пределу при ![]()
![]()
![]() 0,
N
0,
N ![]()
![]() ,
получаем точное выражение для выходного процесса в виде интеграла свертки
,
получаем точное выражение для выходного процесса в виде интеграла свертки
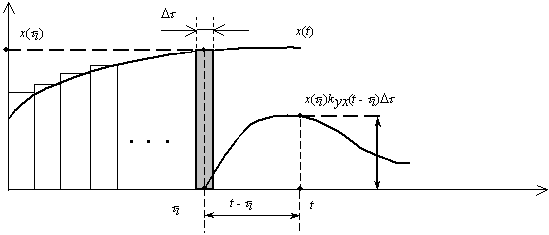
Рис. 25. Реакция системы на произвольное воздействие
Используя условие физической реализуемости (12), верхний предел интегрирования можно заменить на бесконечность и представить интеграл свертки в виде
|
|
(13) |
Обычно в этой форме интеграл и используется, а условие физической реализуемости дополнительно не оговаривается. Между импульсной характеристикой и передаточной функцией системы существует определенная зависимость. Чтобы найти ее, возьмем преобразование Лапласа от интеграла сверки (13). Так как в левой части
![]() ,
,
то изображение выходного процесса
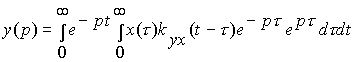 .
.
Здесь мы правую часть искусственно домножили на
![]() .
.
Поменяем порядок интегрирования и сгруппируем подынтегральные сомножители. В результате получим интеграл
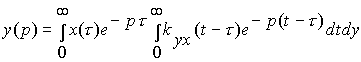 .
.
Во внутреннем интеграле заменим переменную
![]()
и учтем условие физической реализуемости
![]()
при ![]() .
Тогда имеем следующее выражение:
.
Тогда имеем следующее выражение:

В итоге изображение выходного процесса станет равным
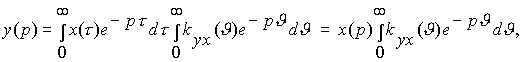
![]()
где учтено, что внешний интеграл является изображением входного воздействия. В то же время мы знаем, что
y(p) = x(p)Kyx(p).
Из сравнения двух равенств вытекает, что
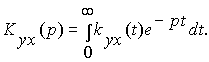
Таким образом, передаточная функция является преобразованием Лапласа от импульсной характеристики. Очевидно, что импульсная характеристика может быть получена по передаточной функции путем обратного преобразования
![]() .
.
Переходной характеристикой hyx(t) называется реакция системы при нулевых начальных условиях на единичную функцию
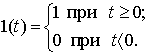
Форма функции hyx(t) у стационарной системы не зависит от момента приложения воздействия и может иметь колебательный или монотонный характер (рис. 26).
С помощью переходной характеристики можно записать интегральное уравнение для выходной переменной, однако, эта формула в ТАУ широкого применения не получила.
В то же время сама функция hyx(t) часто используется для суждения о качестве САУ ввиду того, что она наглядна и легко определяется экспериментально. В дальнейшем будет рассмотрена методика оценки качества по виду переходной характеристики.

Рис. 26. Переходная характеристика
Найдем связь между импульсной и переходной характеристиками, для чего воспользуемся интегралом свертки (1.13), положив в нем x(t) = 1(t):
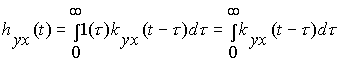 .
.
Проводя замену переменной
![]() ,
,
получим формулу связи в виде
|
|
(14) |
где учтено условие физической реализуемости (12.). Итак, переходная характеристика является интегралом от импульсной характеристики. Продифференцируем по времени обе части (14) и в итоге получим, что
|
|
(15) |
Отсюда следует, что импульсная характеристика является производной по времени от переходной характеристики.
Уравнение (15) в операторной форме запишется в виде
![]() ,
,
откуда получаем связь между изображением hyx(p) для переходной характеристики и передаточной функции системы
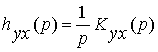 .
.
Используя обратное преобразование Лапласа, получим формулу для нахождения переходной характеристики по передаточной функции в виде
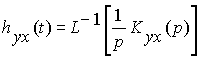 .
.
В теории автоматического управления наибольший интерес представляют переходные характеристики. Графики переходных характеристик наиболее часто встречающихся типовых звеньев приведены в табл.П. 1.
Пример.
Рассмотрим свойства двигателя постоянного
тока с независимым возбуждением. Его схема изображена на рис.
27, где буквой Н показана нагрузка двигателя (редуктор, антенна,
тахогенератор). Пусть j (t) – угол поворота вала двигателя, а ![]() –
угловая скорость вращения.
–
угловая скорость вращения.
При управлении по якорной цепи задающим будет напряжение u(t) на якорной цепи, а напряжение возбуждения uв поддерживается постоянным. Предположим, что инерционностью нагрузки и якоря двигателя можно пренебречь, так что скорость его вращения мгновенно устанавливается пропорциональной напряжению на якоре
|
|
(16) |
где k – коэффициент преобразования двигателя, зависящий от его конструкции. По уравнению (16) находим передаточную функцию двигателя по скорости вращения
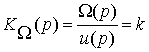 .
.
Мы видим, что передаточная функция безынерционного двигателя по скорости вращения соответствует усилительному звену.

Рис. 27. Схема двигателя постоянного тока
Теперь несколько видоизменим этот пример и будем интересоваться свойствами двигателя не относительно скорости, а относительно угла поворота вала j (t). Напомним, что
![]() ,
,
и используем это равенство в (16).
В итоге придем к уравнению двигателя, где выходной переменной будет угол поворота
|
|
(17) |
Операторное уравнение для этого случая равно
pj (p) = ku(p),
а передаточная функция по углу поворота
|
|
(18) |
Итак, безынерционный двигатель относительно угла поворота соответствует интегрирующему звену. Найдем его переходную и импульсную характеристики, для чего запишем интеграл уравнения (18) при нулевых начальных условиях
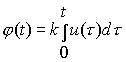 .
.
Полагая, что на вход поступает единичный перепад напряжения
![]() u(t)
= 1(t),
u(t)
= 1(t),
найдем переходную характеристику
 .
.
Для нахождения импульсной характеристики воспользуемся соотношением:
![]() .
.
Графики эти8х функций показаны на рис.28.

Рис. 28. Импульсная и переходная характеристики интегрирующего звена
Пример.
Теперь рассмотрим работу двигателя более подробно и усложним его
математическую модель. Учтем активное сопротивление якоря R и момент инерции нагрузки I. Уравнение электрического равновесия якорной цепи можно записать в виде следующего дифференциального уравнения:
![]() ,
,
где i(t) – ток в цепи якоря; c1W (t) – противоЭДС, пропорциональная скорости вращения W ; с1 – коэффициент, зависящий от конструкции двигателя.
Запишем уравнение равновесия механических моментов
![]() ,
,
где левая часть равна вращающему моменту, а правая – динамическому моменту нагрузки. Полученные уравнения в операторной форме равны
![]() .
.
Из второго уравнения выразим функцию i(p) и подставим в первое, после чего получим, что
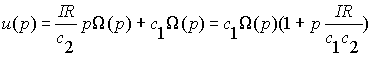 |
(19) |
Обозначим
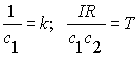 .
.
В результате передаточная функция двигателя по скорости вращения станет равной
![]() ,
,
что соответствует последовательно соединенным усилительному звену k и апериодическому 1/(1+pT). Найдем переходную и импульсную характеристики. Вначале по операторному уравнению (19) с учетом обозначений запишем дифференциальное уравнение двигателя
![]()
![]()
Это дифференциальное уравнение первого порядка. Его интеграл при нулевых начальных условиях
 .
.
Полагая
u(t) = 1(t),
найдем переходную характеристику двигателя
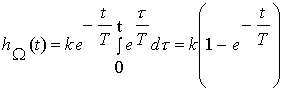 .
.
Импульсная характеристика
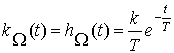 .
.
Графики переходной и импульсной характеристик апериодического звена показаны на рис. 29.
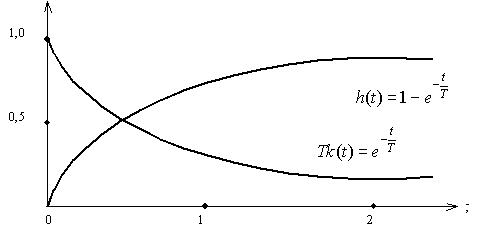
Рис. 29. Импульсная и переходная характеристика апериодического звена
Пример.
Теперь учтем еще один фактор: индуктивность якоря L. Уравнение электрического равновесия якорной цепи усложнится и станет равным
![]() ,
,
а уравнение моментов останется прежним:
![]() .
.
Эти уравнения в операторной форме имеют вид
![]() .
.
Выражая из второго уравнения функцию i(p) и подставляя в первое, получим одно уравнение
|
|
(20) |
Обозначая 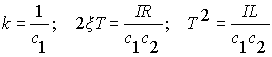 ,
,
получаем передаточную функцию двигателя по скорости
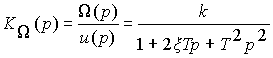 .
.
В рассматриваемом случае двигатель эквивалентен последовательному соединению усилительного и колебательного звеньев. По операторному уравнению (20) запишем дифференциальное уравнение
![]() .
.
Это дифференциальное уравнение второго порядка. На рис. 30. показаны графики переходной характеристики колебательного звена.
В отличие от предыдущих случаев
переходная характеристика колебательного звена зависит от двух параметров: постоянной
времени Т и коэффициента демпфирования ![]() .
Постоянная времени изменяет лишь масштаб функции вдоль оси времени, поэтому
график на рис. 30 построен в относительном времени t/T.
.
Постоянная времени изменяет лишь масштаб функции вдоль оси времени, поэтому
график на рис. 30 построен в относительном времени t/T.
Коэффициент демпфирования существенно
влияет на форму характеристики. При ![]() <
1 переходная характеристика имеет колебательный характер, а при
<
1 переходная характеристика имеет колебательный характер, а при ![]() >= 1 – монотонный. Чем меньше
>= 1 – монотонный. Чем меньше ![]() , тем ярче выражены колебательные свойства.
, тем ярче выражены колебательные свойства.

Рис. 30. Переходная характеристика колебательного звена
В частном случае при ![]() =
0 переходная характеристика становится незатухающей гармонической функцией и
при этом передаточная функция равна
=
0 переходная характеристика становится незатухающей гармонической функцией и
при этом передаточная функция равна
 .
.
Звено такого типа называется консервативным, так как любое воздействие на его входе вызывает незатухающие гармонические колебания. Помимо описанных на практике используются и ряд других звеньев, называемых специальными. Одно из них называется запаздывающим. Уравнение этого звена
![]()
отражает наличие запаздывания сигнала на время t .
Взяв преобразование Лапласа с учетом операции запаздывания, получим передаточную функцию звена в виде
![]() .
.
Как показали примеры, передаточные функции некоторых элементов САУ сразу выражаются через типовые звенья, поэтому передаточная функция всей системы также может быть записана через типовые звенья. Использование такой записи удобно при построениях частотных характеристик, особенно логарифмических. Для этого надо предварительно изучить частотные характеристики самих звеньев.
1.5.2. Частотные характеристики
Частотные характеристики устанавливают связь между спектрами входного процесса x(jw ) и выходного y(jw ). Спектром называется преобразование Фурье
![]()
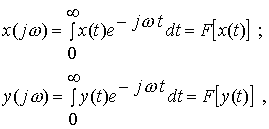
где F – символ преобразования Фурье, а w - действительная переменная, являющаяся частотой гармонического сигнала.
Чтобы найти связь между спектрами, возьмем преобразование Фурье от уравнения (2) при нулевых начальных условиях.
С учетом того, что
![]() ,
,
получаем спектральное уравнение системы
|
c0y(jw ) + c1(jw )y(jw ) + … + cn(jw )ny(jw ) = = b0x(jw ) + b1(jw )x(jw ) + … + bm(jw )mx(jw ). |
(21) |
Приводя подобные члены и решая уравнение относительно выходного спектра, получаем формулу связи спектров в виде
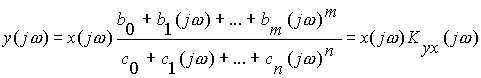 .
.
Отношение полиномов
|
|
(22) |
называется частотной характеристикой системы. Сравнивая выражение (7) для передаточной функции с выражением (1.22), делаем вывод о том, что частотные характеристики и передаточные функции получаются друг из друга путем замены комплексной переменной p на jw и обратно.
Частотные характеристики имеют наглядную физическую интерпретацию. В дальнейшем будем использовать три способа представления частотных характеристик.
При любом значении частоты w функция Kyx(jw ) будет комплексной. Обозначим модуль этой функции через
![]() .
.
Тогда для частотной характеристики, как и для всякой комплексной функции, можно использовать следующее представление:
|
|
(23) |
где модуль Ayx(w ) называется амплитудной частотной характеристикой (АЧХ), а аргумент j yx(w ) – фазовой частотной характеристикой (ФЧХ). АЧХ и ФЧХ являются действительными функциями частоты и поэтому легко отображаются графически. При этом АЧХ определяет относительное изменение амплитуды гармонического воздействия
x(t) = cos w t
при его преобразовании системой, а ФЧХ определяет фазовый сдвиг выходного процесса относительно входного, так что выходной процесс можно записать в виде
![]() .
.
Обе эти характеристики могут быть определены экспериментально достаточно простыми способами.
Для графического построения АЧХ и ФЧХ удобно пользоваться логарифмическими частотными характеристиками
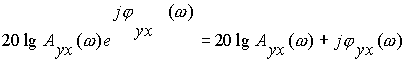 .
.
Функция
Lyx(w ) = 20 lg Ayx(w ),
изображенная в полулогарифмическом масштабе, называется логарифмической амплитудной частотной характеристикой (ЛАХ), а функция j yx(w ), построенная в том же масштабе, называется логарифмической фазовой частотной характеристикой (ЛФХ). Полулогарифмическим называется такой масштаб, когда вдоль горизонтальной оси откладывают значения частоты w в логарифмическом масштабе (lgw ), а по вертикальной оси значения Lyx(w ) и j yxw в линейном масштабе. Единицей измерения Lyx(w ) являются децибелы (дБ), а j yx(w ) - радианы или градусы.
Например, если
Ayx(w ) = 10, то Lyx(w ) = 20 дБ.
Заметим, что при
Ayx(w ) = 1; Lyx(w ) = 0 дБ.
Если Ayx(w ) > 1, то Lyx(w ) > 0 дБ, если же Ayx(w ) < 1, то Lyx(w ) < 0 дБ.
Третьей формой представления частотных характеристик является их изображение на комплексной плоскости. Такие характеристики называются амплитудно-фазовыми (АФХ). Для этого представим комплексную функцию Kyx(w ) в виде суммы ее действительной и мнимой частей
Kyx(jw ) = Ryx(w ) + jIyx(w ),
где Ryx(w ) = ReKyx(jw ); Iyx(w ) = ImKyx(jw ).
Значения Ryx и Iyx откладываются вдоль координатных осей и функция Kyx(jw ) изображается в виде вектора (рис. 31).
При изменении j от 0 до Ґ конец вектора описывает на плоскости некоторую кривую (годограф), которая и является АФХ.
Между АЧХ, ФЧХ и АФХ существует однозначная связь
![]() ;
;
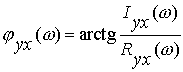 .
.
Таким образом, АЧХ является модулем вектора АФК, а ФЧХ определяет значение ее аргумента. При построении АФХ на годографе стрелкой указывается направление увеличения w .

Рис. 31. Амплитудно-фазовая характеристика
Рассмотрим частотные характеристики усилительного, интегрирующего и идеального дифференцирующего звеньев. На основе передаточных функций можно получить следующие выражения для АЧХ и ФЧХ указанных звеньев
|
|
(24) |
АЧХ этих звеньев в линейном масштабе изображены на рис. 32.
Рассмотрим их изображение в полулогарифмическом масштабе, когда частота w откладывается в логарифмическом масштабе lgw , а амплитуда в линейном масштабе в децибелах (дБ).
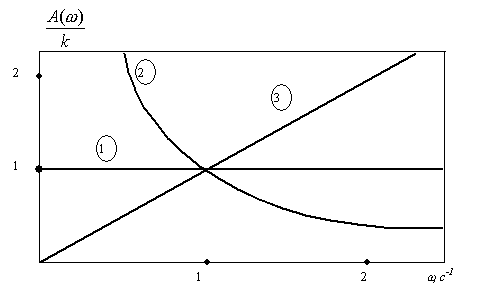
Рис. 32. АЧХ усилительного (1), интегрирующего (2) и идеального дифференцирующего (3) звеньев
Координатная сетка полулогарифмического масштаба приведена на рис. 33.
ЛАХ интегрирующего звена – прямая с отрицательным наклоном, которая пересекает ось 0 дБ в точке w пер, где выполняется равенство
20 lg k – 20 lgw пер = 0.
Отсюда получаем координаты точки пересечения w пер = k.

Рис. 33. ЛАХ усилительного, интегрирующего и идеального дифференцирующего звеньев
Определим наклон этой линии, для чего вначале введем единицу измерения вдоль оси частот с логарифмическим масштабом. В качестве такой единицы обычно используют октаву или декаду.
Октавой называется расстояние между произвольной частотой w и ее удвоенным значением 2w . В логарифмическом масштабе эта величина при любом значении w будет постоянной:
октава = lg 2w - lg w = lg 2.
Декадой называется расстояние между точками w и 10w . Это тоже величина постоянная:
декада = lg 10w - lg w = lg 10 = 1.
Крутизна наклона прямой в полулогарифмическом масштабе может измеряться в децибелах на октаву или декаду (дБ/окт, дБ/дек). Найдем крутизну ЛАХ интегрирующего звена в этих единицах. Приращение ЛАХ интегрирующего звена D L на октаву или декаду будет равно
![]() Lокт
= Lи(2w ) – Lи(w ) = 20lg k – 20lg
2w - 20 lg k +
Lокт
= Lи(2w ) – Lи(w ) = 20lg k – 20lg
2w - 20 lg k +
+ 20 lg w = -20 lg2 = - 6 дБ;
![]() Lдек
= Lи(10w ) - Lи(w ) = 20 lg k – 20 lg
10w - 20 lg k + 20 lg w =
Lдек
= Lи(10w ) - Lи(w ) = 20 lg k – 20 lg
10w - 20 lg k + 20 lg w =
= -20 lg 10 = - 20 дБ.
Таким образом, наклон прямой Lи(w ) интегрирующего звена равен –6 дБ/окт или –20 дБ/дек. Теперь обратимся к ЛАХ идеального дифференцирующего звена. Из уравнения для нее видно, что это будет прямая с положительным наклоном, равным +6 дБ/окт или +20 дБ/дек. Точка пересечения этой прямой с осью 0 дБ находится из условия
20 lg k + 20 lg w пер
= 0, откуда![]()
![]() .
.
Логарифмические амплитудные частотные характеристики трех указанных звеньев показаны на рис. 33. Логарифмические фазовые частотные характеристики, как следует из выражения (24), соответственно равны 0, -p \2, +p \2. Эти характеристики показаны на рис. 34.

Рис. 34. ЛФХ усилительного, интегрирующего и идеального дифференцирующего звеньев
Как мы увидим в дальнейшем, наклоны ЛАХ остальных типовых звеньев будут кратными величине 6 дБ/окт (20 дБ/дек). Поэтому наклон ± 6 дБ/окт в дальнейшем будем обозначать индексом ± 1.
Тогда наклоны: ± 12 дБ/окт = ± 2, ± 18 дБ/окт = ± 3 и т.д.
Рассмотрим частотные характеристики апериодического и дифференцирующего звена первого порядка. Выражения для АЧХ и ФЧХ этих звеньев будут иметь вид:
|
|
(25) |
Форма АЧХ звеньев в линейном масштабе показана на рис. 35.
Логарифмические амплитудные характеристики равны:
|
|
(26) |
Сразу отметим, что эти функции, как и ФЧХ из соотношений (25), отличаются только знаком, поэтому достаточно рассмотреть логарифмические характеристики только апериодического звена.
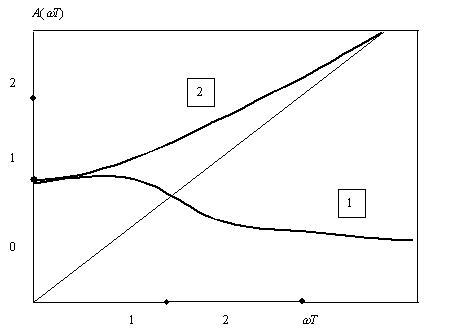
Рис. 35. АЧХ апериодического (1) и дифференцирующего (2) звена первого порядка
Аналитические выражения ЛЧХ апериодического звена сложнее, чем у предыдущих. Для приближенного построения ЛАХ удобно воспользоваться так называемым асимптотическими характеристиками. Рассмотрим область низких частот, где w T < < 1 или w < < 1/Т.
Для этой области из формулы (26) следует приближенное выражение для низкочастотной асимптоты
La(w ) = -20 lg 1 = 0 дБ.
В области высоких частот при w Т > > 1 или w > > 1/Т уравнение высокочастотной асимптоты
La(w ) = -20 lg w T = - 20 lg T – 20 lg w .
Из этого уравнения сразу следует, что высокочастотная асимптота ЛАХ будет прямой с наклоном –1, так как ее выражение пропорционально значению –lg w , как и у интегрирующего звена (рис. 36).

Рис. 36. Асимптотическая ЛАХ апериодического и дифференцирующего звена первого порядка
Найдем точку пересечения высокочастотной асимптоты с низкочастотной, равной 0 дБ. Она следует из равенства
-20 lg T – 20 lg w пер = 0.
Отсюда находим точку пересечения
![]() ,
,
которая называется опорной частотой звена. Таким образом, построить асимптотическую ЛАХ апериодического звена достаточно просто: до опорной частоты 1\Т она идет вдоль оси 0 дБ, а затем по прямой с наклоном –1.
Оценим, насколько асимптотическая ЛАХ отличается от точной. До опорной частоты 1/Т эта разность равна
![]() ,
,
а после опорной частоты
![]() .
.
Можно показать, что эта разность максимальна на опорной частоте и равна
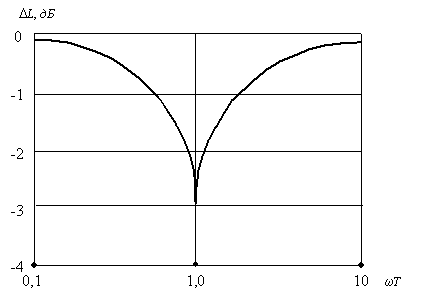
Рис. 37. График поправок для ЛАХ апериодического звена
На рис. 37 показан график поправок D L(w ) для асимптотической ЛАХ апериодического звена, построенный в полулогарифмическом масштабе для относительных значений переменной w Т. После построения асимптотической ЛАХ этот график можно использовать для построения точной характеристики.
Подходящим образом упростить выражение для фазовой частотной характеристики апериодического звена
j а(w ) = -arctg w T
не представляется возможным. Эта характеристика строится с помощью специальных таблиц или номограмм. Отметим, что ФЧХ изменяется в пределах от 0 до -p /2 и на опорной частоте
 .
.
Логарифмическая фазовая частотная характеристика апериодического звена приведена на рис. 38. Логарифмические характеристики дифференцирующего звена первого порядка отличаются от рассмотренных только знаком и показаны на рис. 36 и рис. 38. Для уточнения асимптотической ЛАХ дифференцирующего звена можно пользоваться графиком на рис.37, но при этом знак поправки надо заменить на противоположный.
Перейдем к рассмотрению характеристик колебательного и дифференцирующего звена второго порядка. АЧХ и ФЧХ для этих звеньев равны:

Отсюда находим логарифмические амплитудные частотные характеристики

Рис. 38. ЛФХ апериодического и дифференцирующего звена первого порядка
Частотные характеристики этих звеньев
зависят от двух параметров: постоянной времени Т и коэффициента демпфирования
![]() . Так,
АЧХ колебательного звена при
. Так,
АЧХ колебательного звена при ![]() <
1 имеет резонансный, а при
<
1 имеет резонансный, а при ![]() >=1
– апериодический характер. На рис. 39 эти характеристики показаны
в линейном масштабе.
>=1
– апериодический характер. На рис. 39 эти характеристики показаны
в линейном масштабе.

Рис. 39. АЧХ колебательного звена
Уравнение низкочастотной асимптоты ЛАХ колебательного звена при w Т < < 1 имеет вид
Lк(w ) = -20 lg 1 = 0 дБ.
Высокочастотная асимптота при w Т > > 1 равна
Lк(w ) = -20 lg w 2T2 = -40 lg T – 40 lg w .
Итак, низкочастотная асимптота колебательного звена идет вдоль оси 0 дБ, а высокочастотная является прямой с отрицательным наклоном. Так как она пропорциональна величине –40 lg w , то ее наклон равен –12 дБ/окт или просто –2. Точка пересечения асимптот находится из равенства откуда w пер = 1/Т, то есть вновь является опорной частотой.

Рис. 40. Асимптотическая ЛАХ колебательного звена
Асимптотическая ЛАХ колебательного
звена показана на рис. 40. Эта функция не зависит от величины
![]() и поэтому
аппроксимирует точную характеристику достаточно грубо. График поправок для построения
точной ЛАХ показан на рис. 41, где приводится семейство
кривых при различных значениях
и поэтому
аппроксимирует точную характеристику достаточно грубо. График поправок для построения
точной ЛАХ показан на рис. 41, где приводится семейство
кривых при различных значениях ![]() .
Фазовая частотная характеристика колебательного звена изменяется в пределах
от 0 до -
.
Фазовая частотная характеристика колебательного звена изменяется в пределах
от 0 до -![]() и
на опорной частоте равна -
и
на опорной частоте равна -![]() \2.
\2.
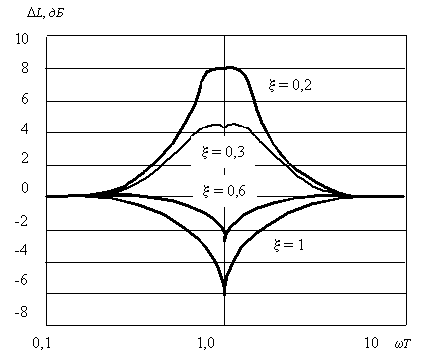
Рис. 41. График поправок для ЛАХ колебательного звена
Ход этой функции зависит от величины
![]() (рис.
42). Для ее построения используются таблицы и номограммы. Характеристика
дифференцирующего звена второго порядка отличается от только что рассмотренных
лишь знаком.
(рис.
42). Для ее построения используются таблицы и номограммы. Характеристика
дифференцирующего звена второго порядка отличается от только что рассмотренных
лишь знаком.

Рис. 42. ЛФХ колебательного звена
В заключение рассмотрим частотные характеристики запаздывающего звена
Kз(jw ) = e-jw t .
Отсюда видно, что его АЧХ и ФЧХ равны:
Аз(w ) = 1; j з(w ) = -w t .
Таким образом, построение логарифмических частотных характеристик типовых звеньев (особенно асимптотических характеристик) – задача достаточно простая.
1.5.3. Управляемость и наблюдаемость САУ
Управляемость и наблюдаемость линейных
систем регулирования относятся к основным понятиям теории автоматического регулирования,
с помощью которых можно оценивать структурные схемы систем и выполнять их преобразование
путем ввода дополнительных сигналов или за счет их исключения. Если в системе
автоматического регулирования сигнал управления x(t) представляет
собой некоторую совокупность его составляющих x1(t),
…xm(t) и не превышает число ![]() степенной
свободы системы, описанной уравнением
степенной
свободы системы, описанной уравнением ![]() ,
то система является неуправляемой. Действительно, в этом случае систему регулирования
нельзя перевести из начального состояния y(t0) в любое
время в конечное состояние y(t1) под действием некоторого
входного сигнала х(t). При r > m системы именуют вполне
управляемыми.
,
то система является неуправляемой. Действительно, в этом случае систему регулирования
нельзя перевести из начального состояния y(t0) в любое
время в конечное состояние y(t1) под действием некоторого
входного сигнала х(t). При r > m системы именуют вполне
управляемыми.
Линейную стационарную систему автоматического регулирования называют полностью управляемой, если из любого начального состояния ее можно перевести в конечное состояние при помощи входного сигнала в течение конечного интервала времени. Необходимое и достаточное условие полной управляемости линейной стационарной системы, описываемой уравнением
![]() ,
,
таково: матрица
![]()
размера n ґ nm, первые m столбцов которой состоят из элементов матрицы В, а следующие m столбцов – из элементов матрицы АВ и т.д., должна иметь ранг n.
С понятием управляемости связано понятие наблюдаемости системы. Наблюдаемость позволяет установить начальное состояние системы автоматического регулирования по результатам измерений одного выходного сигнала.
Линейная стационарная система автоматического регулирования, описываемая уравнениями

полностью наблюдаема, если можно определить начальное состояние y(0) системы по следующим данным:
а) матрицам А и С;
б) выходному сигналу y(t) от начальных условий y(0) при x(t) = 0, заданному на конечном интервале [ 0, tp] .
Необходимое и достаточное условие полной наблюдаемости линейной стационарной системы заключается в том, что сопряженная матрица
![]()
типа n x nr должна иметь ранг n.
Предыдущий
пункт | Наверх | Следующий пункт
| Оглавление |