![]() ;
;
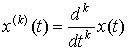 ;
;
 ,
,
(1)
1.3. Математические модели САУ. Формы представления моделей
1.3.1. Математическое описание САУ
Гипотезы и аналоги, отражающие реальный, объективно существующий мир, должны обладать наглядностью или сводиться к удобным для исследования логическим схемам: такие логические схемы, упрощающие рассуждения и логические построения или позволяющие проводить эксперименты, уточняющие природу явлений, называются моделями. Другими словами, модель (лат. modulus – мера) – это объект – заместитель объекта – оригинала, обеспечивающий изучение некоторых свойств оригинала.
Под математическим моделированием будем понимать процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта. Вид математической модели зависит как от природы реального объекта, так и задач исследования объекта и требуемой достоверности и точности решения этой задачи.
Для математического моделирования линейных непрерывных САУ используются дифференциальные уравнения.
В непрерывных системах как входные воздействия, так и выходные процессы являются непрерывными функциями. Связь между ними отображается посредством дифференциальных уравнений, имеющих следующий вид:
|
|
(1) |
гдеx(t) иy(t) – задающее воздействие и выходной процесс, а переменные ![]() -
их производные. Если функцииF1 иF2 – нелинейны
относительно переменных, то системы будут нелинейными.
-
их производные. Если функцииF1 иF2 – нелинейны
относительно переменных, то системы будут нелинейными.
В линейных системахF1 иF2 – линейные функции. Если они явно зависят от времениt, то системы будут
нестационарными. В случае стационарных систем явная зависимость функций![]() и
и![]() от времени отсутствует.
Величина старшей производнойn при выходной переменной в левой части уравнения называется порядком уравнения или порядком системы.
от времени отсутствует.
Величина старшей производнойn при выходной переменной в левой части уравнения называется порядком уравнения или порядком системы.
Если стационарная система допускает линеаризацию своих уравнений, то она описывается линейным дифференциальным уравнением следующего вида:
|
|
(2) |
где с иb – постоянные коэффициенты, зависящие от параметров системы. Все переменные входят в это уравнение линейно, что обеспечивает системе применимость принципа суперпозиции.
Так, если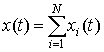 ,
то выходной процесс
,
то выходной процесс , где
каждой паре xi(t) и yi(t)
соответствует уравнение (2).
, где
каждой паре xi(t) и yi(t)
соответствует уравнение (2).
Примером уравнения (2) является линеаризированное уравнение:
![]() .
.
Если обозначить
![]()
то мы получим частный случай уравнения (2).
Анализ линейной стационарной системы сводится к нахождению функцииy(t) по заданному воздействиюx(t). Иначе говоря, анализ САУ требует нахождения решения уравнения (2). Из соответствующих разделов высшей математики известно, что решение уравнения (2) состоит из двух слагаемых:
![]() ,
,
гдеyп(t) переходная составляющая решения или переходный процесс системы, который находится из решения однородного уравнения
|
|
(3) |
при нулевых начальных условиях для самого процесса и его первых (n-1) производных.
Поясним смысл переходного процесса в САУ на примере следящей системы ФАП. Линеаризованное уравнение этой системы равно
|
|
(4) |
где x(t) = jx(t) – фаза входного воздействия генератора сигнала ГС, а y(t) = = jy(t) – фаза выходного сигнала подстраиваемого генератора ПГ.
Пусть задающее воздействие x(t)
= 0, а в момент включения системы при t = 0 выходная фаза
y(t) ![]() 0.
0.
Благодаря наличию начального рассогласования
![]()
система начинает работать, стремясь обеспечить значение фазы выходного
процесса y(t) = x(t) = 0. Это и будет переходный процессy П(t).
Так как по условию воздействиеx(t) = 0, то уравнение (4) для переходного процесса примет вид
![]() ,
,
что является однородным уравнением для (4).
Его решение легко находится и имеет вид
![]() .
.
Экспоненциальный характер переходного процесса показан на рис. 11.
Рис. 11. Переходный и вынужденный процессы в системе ФАП
Теперь займемся вынужденным процессомyв(t). Он определяется только задающим воздействиемx(t) при нулевых начальных условиях в системе. Для нахожденияyв(t) надо определить частное решение неоднородного уравнения
|
|
(5) |
при нулевых начальных условиях и заданной функцииx(t).
Для рассмотрения системы ФАП уравнение вынужденного процесса примет вид
![]() .
.
Для примера положим
![]()
Воспользовавшись выражением общего решения дифференциального уравнения первого порядка, можно записать, что
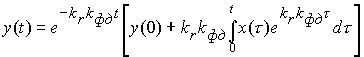 .
.
Отсюда легко получить вынужденный процесс ФАП, полагая
y(t) = 0; x(t) = a0 + a1t:
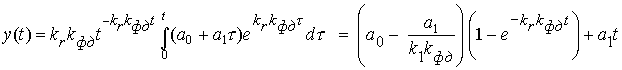 .
.
Характер этой зависимости показан на рис. 11. С течением времени при t выходной процесс будет стремиться к функции
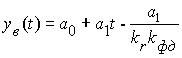 ,
,
то есть фаза выходного сигнала будет меньше фазы входного на величинуa1/krkфд и система слежения будет работать с некоторой ошибкой.
Важно подчеркнуть, что благодаря нулевым начальным условиям вынужденный процессyв(t) начинается с нуля.
На основании принципа суперпозиции итоговый процесс в системе
y(t) = yп(t) + yв(t).
Таким образом, исследование линейных стационарных систем автоматического управления сводится к отдельному исследованию характеристик переходных и вынужденных процессов, методы определения которых, как правило, оказываются различными.
Возьмем преобразование Лапласа от обеих частей уравнения (2) с учетом нулевых начальных условий и известного правила
![]() .
.
В итоге получим оперативное уравнение САУ
![]() .
.
Решая его относительно изображения выходной переменной, получим
|
|
(6) |
Таким образом, использование преобразования Лапласа переводит дифференциальное уравнение во временной области в алгебраическое уравнение в области комплексной переменнойp, которое легко решается. В этом главное преимущество использования операторного метода.
Чтобы от изображенияy(p) перейти к оригиналуy(t), надо взять обратное преобразование Лапласа
![]() .
.
Однако искать обратное преобразование от функции y(p) не всегда необходимо, так как ряд свойств функции y(t) можно найти непосредственно по ее изображению.
|
|
(7) |
назовем передаточной функцией системы по задающему воздействию.
Нижние индексы отражают те процессы, между которыми устанавливает соответствие данная передаточная функция. Полиномы числителя P(p) и знаменателя D(p) передаточной функции легко находятся по исходному дифференциальному уравнению (2). Из уравнения (7) следует, что передаточная функция является отношением изображений выходного процесса и входного при нулевых начальных условиях.
Передаточные функции могут определяться для различных воздействий в различных точках их приложения и по отношению к различным процессам внутри системы. Так, на рис. 12. показана система с несколькими воздействиями.
Для нее помимо передаточной функции по задающему воздействию
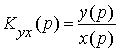
можно ввести и передаточные функции по возмущающим воздействиям, которые обозначим следующим образом:
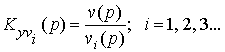
Здесь нижние индексы говорят о том, что интересуются выходным процессомy(t) при различных возмущающих воздействияхvi(t).
В некоторых задачах приходится интересоваться не выходным процессом, а некоторыми переменными внутри системы, напримерyос(t), u(t) и др.(рис. 12). Передаточные функции можно определять и по отношению к
Рис. 12. Схема САУ с несколькими воздействиями этим переменным.
Так, можно, в частности, записать передаточные функции.
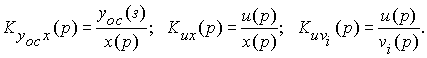
Нахождение этих передаточных функций требует знания ряда правил и соответствующего изображения схемы САУ.
1.3.3. Формы представления моделей
Выше указывалось, что для анализа систем автоматического управления и регулирования широко используется моделирование. Формы представления моделей САУ могут быть самыми различными. Среди них наиболее распространенными являются:
представление в форме аналоговых моделей для последующей реализации с использованием операционных усилителей.
Предыдущий
пункт | Наверх | Следующий пункт
| Оглавление |