1.2.1. Классификация САУ по принципам управления
Принципы управления являются одним из признаков классификации САУ и определяются
объемом информации, используемым управляющим устройством для выработки управляющих
воздействий. Различают принципы управления по разомкнутому циклу, по замкнутому
циклу и комбинированный принцип управления.
При управлении по разомкнутому циклу для формирования
управляющих воздействий необходима только информация о задающем и иногда о некоторых
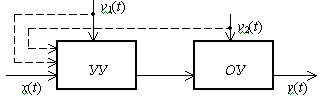
возмущающих воздействиях. Блок-схема такой системы показана на рис.3,
ее особенностью является отсутствие контроля за поведением объекта управления.

Рассмотрим пример
простейшей системы, работающей на этом принципе. На рис. 4.
изображена схема управляемого генератора постоянного напряжения, работающего
следующим образом. С помощью потенциометра П снимается напряжениеx, питающее
обмотку возбуждения ОВ генератора постоянного напряжения Г, ротор которого вращается
с постоянной скоростью w .
Взаимодействие магнитного потока, создаваемого обмоткой возбуждения и обмоткой
ротора, приводит к появлению ЭДС e на щетках генератора. Полагая нагрузку
выходной цепи генератора активным сопротивлениемRн, получим
на нем напряжениеy, контролируемое вольтметромV. При всех постоянных
факторах, таких, как сопротивление нагрузкиRн, скорость вращения
ротора w и др., напряжение y будет зависеть от величины x. Управление
выходной величиной y будет осуществляться с помощью задающего воздействия
x.
Рис. 4. Схема генератора напряжения без обратной связи
Предположим, что мы установили требуемое значение напряжения y, однако после этого величина нагрузки Rн, скачкообразно изменилась (рис. 5.).
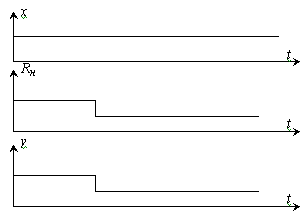
Это приведет
к тому, что при прежней величине x выходное напряжение y изменится,
так как оно зависит от сопротивления нагрузки:

где
Rr - сопротивление
выходной цепи генератора.
Падение этого напряжения никак не отразится на характере
управления. Таким образом, при прежнем значении задающего воздействия x
выходная координата y изменится за счет изменения внешнего воздействия
(нагрузки). Этот пример показывает, что в системах, работающих по разомкнутому
циклу, нежелательные отклонения выходного процесса управляющим устройством не
учитываются и не компенсируются. Для улучшения качества системы можно было бы
измерять величину сопротивления нагрузки и в соответствии с этим изменять величину
x. Очевидно, что техническая реализация подобного способа сложна, тем
более, что ряд возмущающих воздействий измерить невозможно или измерения могут
проводиться с большими погрешностями. Рассмотренный пример позволяет утверждать,
что качество систем, работающих по разомкнутому циклу, как правило, невысокое,
а возможности измерения возмущающих воздействий для компенсации их вредного
влияния ограничены. По этим причинам принцип управления по разомкнутому циклу
нашел ограниченное применение на практике.
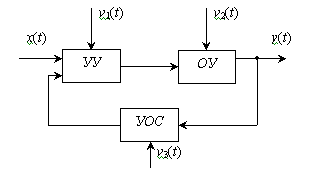
При управлении по замкнутому циклу управляющее устройство
использует информацию как о задающем воздействии x, так и о значениях
выходных координат объекта y. Эта информация поступает через устройство
обратной связи (УОС). Блок-схема системы изображена на рис.6.
Влияние возмущающих воздействий в таких системах оценивается путем контроля
за текущими значениями выходных координат. В управляющем устройстве эта информация
сравнивается с желаемым законом изменения y(t) и в соответствии с этим
вырабатываются управляющие воздействия, корректирующие ход изменения выходных
координат объекта.
Рассмотрим
простейший пример системы такого рода. На рис. 7. изображена
схема генератора постоянного напряжения с обратной связью. В ее основе лежит
схема, ранее изображенная на рис. 4. Особенности работы состоят
в следующем. Выходное напряжение y подается на обмотку соленоида С, и
в зависимости от значения этого напряжения сердечник соленоида, прикрепленный
с одной стороны к пружине Пр, будет либо больше, либо меньше втягиваться
внутрь соленоида. К тяге, стоящей между сердечником и пружиной, может крепиться
движок задающего потенциометра. После установки желаемого напряжения y движок
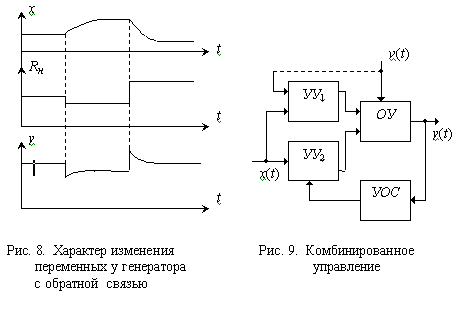
потенциометра закрепляется на тяге сердечника. Если по каким-либо причинам произошло
уменьшение напряжения y (например, при уменьшении Rн), то сердечник соленоида выдвинется из соленоида и сместит
движок потенциометра вверх. Напряжение возбуждения увеличится и тем самым возрастет
напряжение y (рис. 8.) Параметры соленоида можно подобрать
так, чтобы уменьшение напряжения y за счет изменения сопротивления нагрузки
Rн скомпенсировалось увеличением напряжения возбуждения. Таким
же образом будет работать система и при непреднамеренном увеличении y,
только при этом напряжение возбуждения x уменьшится. Важно подчеркнуть,
что причины, которые нарушили нормальную работу этой системы, не играют роли,
так как управление происходит путем измерения конечного эффекта управления –
выходного напряжения y. Как и в предыдущем примере, рассматриваемая система
работает без участия человека, то есть автоматически. Однако за счет включения
устройства обратной связи через соленоид качество работы можно значитель-но
повысить, что видно из сравнения рис. 5. и рис.
8.
Обобщая выводы
из последнего примера, можно сказать, что в системах, работающих по замкнутому
циклу, происходит автоматическая компенсация влияния возмущающих воздействий
без их непосредственного измерения. Она осуществляется за счет измерения выходных
координат объекта управления и сравнения их с желаемыми значениями. Управляющие
воздействия вырабатываются на основе этого сравнения.
Системы с замкнутым циклом управления обладают более
высоким качеством и поэтому нашли широкое практическое применение. Благодаря
наличию устройства обратной связи они называются системами с обратной связью,
или замкнутыми системами.
В случае использования комбинированного принципа, управляющее
устройство содержит два канала: один из них работает на принципе разомкнутого
цикла, а другой – на принципе замкнутого. Блок-схема подобной системы показана
на рис. 9. Системы такого рода соединяют в себе свойства предыдущих
систем.
Классификация по принципам управления отражает фундаментальные
идеи, положенные в основу построения САУ, и определяет общую структуру системы.
Теория автоматического управления имеет дело с математическими моделями, отражающими свойства реальных систем посредством математических соотношений. Всякая математическая модель способна описать систему лишь приближенно с учетом различного рода допущений. На практике стремятся выбрать модель по возможности наиболее простую, что сокращает усилия на ее исследования. Противоречие между простотой модели и степенью ее приближения к оригиналу является обычной трудностью любой теории, в том числе и ТАУ. Непременным требованием при выборе модели считается соответствие изучаемых в ней процессов тем, которые протекают в реальной системе. Если такого соответствия нет, то исследования теряют всякий смысл. Наиболее достоверным признаком пригодности выбранной модели будет сравнение полученных с ее помощью теоретических результатов с результатами экспериментальной проверки реальной системы. В некоторых случаях допустимо сравнение с данными, полученными путем исследования более точных моделей. Таким образом, само понятие модели является условным, зависящим от характера задач и условий их решения. Естественно, что классификация САУ по виду их математических моделей в некотором смысле также будет условной. В самом общем виде математической моделью САУ является оператор преобразования воздействий. Оператором системы называется преобразование, где каждой функции, определяющей закон изменения воздействия, ставят в соответствие другую функцию, определяющую закон изменения выходных координат. Формально это преобразование, например для задающего воздействия, обозначается как
где s(t) – оператор системы по задающему воздействию. Аналогично определяются
и операторы по другим воздействиям. В настоящее время отсутствуют общие методы
нахождения операторов желаемой степени сложности и точности для всех классов
систем. В этой части большую роль играют опыт и способности исследователя.
Однако по ряду частных задач приемы составления математических моделей
достаточно хорошо отработаны и экспериментально подтверждена удовлетворительная
точность получаемых при этом результатов. Так как теория автоматического
управления имеет дело с математическими моделями, то в дальнейшем, упоминая о
системах, будем подразумевать, что речь идет об их математических моделях,
адекватность которых реальным системам считается доказанной.
В первую очередь системы
подразделяются на линейные и нелинейные. Линейной называется такая система, для
которой справедлив принцип суперпозиции. Этот принцип для оператора системы
записывается следующим образом:
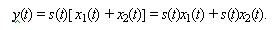
Все остальные системы относятся к
нелинейным. Подобное подразделение имеет практическое значение. Теория линейных
систем существенно проще и разработана значительно подробнее, чем теория
нелинейных, поэтому при ее составлении модели системы стремятся выбрать ее в
классе линейных, что значительно упрощает методику исследования. Конечно, и
здесь должно выполняться условие адекватности модели реальным исследуемым
явлениям с необходимой степенью точности.
Информация о процессах, протекающих в
устройствах системы, передается посредством сигналов различной физической
природы: электрических, механических и других. При этом сама информация может
быть закодирована в сигналах различным способом. Если все сигналы в системе
можно рассматривать как непрерывные, то и сами системы называются непрерывными.
Однако в ряде случаев информацию целесообразно передавать с помощью дискретных
сигналов, например в виде импульсов напряжения или в цифровом коде, и тогда
системы называются дискретными. Часто в одной и той же системе бывают как
непрерывные, так и дискретные сигналы. Тогда системы называются
дискретно-непрерывными или гиб-ридными.
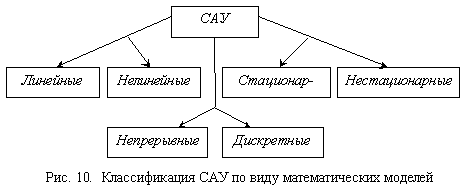
Если свойства системы с течением времени изменяются
и оператор системы s(t) зависит от времени, то системы называются нестационарными,
а при неизменных свойствах оператора – стационарными. Основные классы автоматических
систем с точки зрения их математических моделей показаны на рис.
10.
Для систем с сосредоточенными
параметрами, которые рассматриваются в данной теме, наиболее удобной формой
представления операторов являются уравнения. При описании непрерывных систем
используются дифференциальные уравнения, а дискретных – разностные уравнения;
линейные системы описываются линейными уравнениями, нелинейные – нелинейными; у
стационарных систем уравнения имеют постоянные коэффициенты, а у нестационарных
– переменные.
В итоге исследование САУ
сводится к явному или неявному нахождению решений соответствующих уравнений. С
помощью дифференциальных и разностных уравнений удается отразить такие
характерные особенности систем, как инерционность и временной характер
процессов, протекающих в них. Инерционность выражается в том, что система не
может мгновенно реагировать на внезапно приложенное к ней воздействие, а его
отработка происходит с некоторым запаздыванием и по форме будет отличаться от
исходного воздействия. Инерционные системы называются динамическими, а сама ТАУ
является разделом теории динамических систем.
Методы решения уравнений различных классов
разработаны неодинаково. Наиболее подробно изучены методы решения линейных
уравнений, особенно с постоянными коэффициентами, и значительно меньше
разработаны методы решения нелинейных уравнений. Все это однозначно определяет и
степень развития различных разделов ТАУ. Так, если теория линейных стационарных
систем разработана достаточно полно, то теория нелинейных систем, особенно
нестационарных, разработана лишь в отдельных аспектах. Все эти соображения
существенно сказываются на методологии изложения ТАУ.
На
практике использование линейных систем часто дает определенные преимущества в
качестве управления. Поэтому имеющиеся реальные систе-мы во многих случаях
работают в линейном режиме. Все это делает теорию линейных систем
фундаментальной частью всей теории автоматического управления.
Таким образом, классификация САУ по виду
их математических мо-делей играет особую роль, так как она определяет структуру
изложения теории автоматического управления и тем самым влияет на качество
усвое-ния учебного материала.
1.2.3. Классификация САУ по целевому назначению и другим признакам
В зависимости от числа регулируемых величин системы автоматического управления подразделяют на одномерные (одна регулируемая величина), двумерные (две регулируемые величины) и многомерные (прип регулируемых величинах).
Многомерные системы могут быть системами несвязанного и связанногорегулирования. В системе несвязанного регулирования регуляторы, управляющие различными переменными, не связаны одни с другими и работают независимо. В системе связанного регулирования регуляторы связаны между собой, и для нормальной работы требуется их вполне определенное взаимодействие. Систему связанного регулирования называют автономной, если существуют такие связи между регуляторами, когда изменение одной из регулируемых величин не вызывает изменения остальных.
Понятие цели управления является исходным в ТАУ, поэтому классификация по этому признаку играет важную роль. При обоснованиях цели управления будем сопоставлять задающее воздействиеx(t) с тем желаемым выходным процессомy(t), который мы хотели бы получить при идеальной работе системы. Это удается сделать, если ввести понятие идеального оператора системыsи(t), и тогда желаемый выход
y(t) = sи(t)x(t).
Классификация систем по целевому назначению сводится к выделению определенных классов операторовsи(t). Строго говоря, число классов САУ, выделяемых по указанному признаку, может быть бесконечно большим. Рассмотрим важнейшие из них, имеющие наибольшее значение на практике.
Следящими называются системы, целью управления в которых является поддержание равенства
y(t) = x(t),
то есть в таких системах идеальный оператор преобразования
sи(t) = 1.
Примеры следящих систем многочисленны. Они используются там, где требуется безыскаженная передача какого-либо воздействия, например напряжения, угла поворота вала, цифровой последовательности и т.д. Такая необходимость обычно вызывается двумя причинами: либо необходимостью передачи воздействия на некоторое расстояние, либо преобразованием этого воздействия с усилением по мощности. Для следящих систем предполагается, что входная и выходная переменные должны иметь одну и ту же физическую природу (напряжение, угол поворота, давление и т.д.).
Очень часто встречаются задачи, когда наряду с отслеживанием входного воздействия требуется его преобразование к иной форме представления, например слежение за углом поворота вала с выдачей данных в виде напряжения. В таких системах выходная переменная становится пропорциональной воздействию, то есть принимает вид
y(t) = kx(t),
гдеk – некоторый масштабный коэффициент.
Системы такого рода называются масштабными, а их оператор преобразования
sи(t) = k
является постоянным коэффициентом с определенной размерностью.
Системы следующего класса называются стабилизирующими. Это такие системы, у которых выходная координата должна поддерживаться на постоянном уровне, то есть
y(t) = const.
Различного рода стабилизаторы напряжения, тока, скорости вращения вала и другие подобные системы, работающие в автоматическом режиме, являются примерами систем подобного класса и часто встречаются на практике.
Интегрирующими называются системы, у которых должно выполняться соотношение
 .
.
Идеальный оператор в этом случае является интегральным. К дифференцирующим относятся системы, у которых выходная переменная
![]() ,
,
то есть соответствует производной от воздействия. Оператор системы в этом случае является дифференциальным.
Очевидно, что число примеров систем, классифицируемых по описанному выше способу, можно продолжить. В целом, надо отметить, что любая из автоматических систем должна обладать некоторыми преобразующими свойствами, а ее оператор может быть представлен либо в виде некоторой функции
y(t)= F[ x(t)] ,
либо в виде функционала
 .
.
Легко видеть, что приведенные выше примеры укладываются в эти записи. По своей роли в технике наибольшее значение имеют следящие системы, поэтому в дальнейшем изложении делается упор на теорию систем именно этого класса. Нужно отметить, что результаты теории следящих систем сравнительно просто обобщаются на системы других классов.
Помимо описанных признаков существует и ряд других, по которым также проводится классификация. Коротко отметим некоторые из них.
По степени полноты информации, имеющейся к началу управления, о характеристиках воздействий и параметрах объекта управления системы подразделяются на адаптивные и сжестким законом управления. В адаптивных системах управляющее устройство помимо выработки управляющих воздействий осуществляет обработку поступающей на его вход текущей информации о свойствах объекта и воздействий и на этой основе изменяет структуру и параметры системы с целью повышения качества управления. Таким образом, в процессе работы такие системы приспосабливаются к настоящему времени. В системах с жестким законом управления алгоритм работы определяется заранее на весь период управления.
По качеству управления системы могут быть оптимальными и неоптимальными. Оптимальными называются такие системы, которые среди однотипных систем, работающих в одинаковых условиях, наилучшим образом достигают цель управления. Иначе говоря, оптимальные – это системы с наивысшим качеством управления. Имеются и иные, менее важные признаки классификации, на которых мы останавливаться не будем.
Предыдущий
пункт | Наверх | Следующий пункт
| Оглавление |