
Как известно, выходной процесс системы состоит из суммы двух слагаемых:
y(t) = yп (t) + yв(t),
где yв(t) - вынужденный процесс, определяемый задающим воздействием, а yп(t) - переходный процесс, зависящий от начальных условий. Чтобы не усложнять изложения, мы не учитываем в приведенном соотношении возмущающих воздействий. В устойчивой следящей системе переходный процесс с течением времени стремится к нулю, а вынужденный должен быть близок к x(t), исходя из целевого назначения САУ. Примерный вид этих процессов показан на рис. 51.
Из рисунка видно, что можно выделить два участка или режима работы системы, при малых интервалах после начала управления и при больших. Эти режимы отличаются характером процессов и значением ошибок управления. Для начального интервала времени режим называется переходным. В этом режиме вынужденный процесс изменяется от нулевого значения до близкого к задающему x(t), а переходный процесс изменяется от начального значения до нуля. В переходном режиме ошибки управления особенно велики.

Рис.51. Режимы работы системы
Определить границу переходного режима tп можно несколькими способами, так как это понятие условное. Строго говоря, переходный процесс yп(t) длится бесконечно долго, стремясь к нулю. Обычно величину tп связывают с моментом практического окончания переходного процесса, когда
yп(tп ) << y(0).
При дальнейших рассуждениях полагаем, что величина tп тем или иным способом определена.
После окончания переходного режима наступает установившийся режим, когда на выходе практически имеется только вынужденная составляющая yв(t), близкая к x(t). В установившемся режиме ошибки управления значительно меньше. Это основной режим работы любой автоматической системы. В процессе проектирования стремятся выбрать структуру и параметры системы так, чтобы снизить до допустимого уровня ошибки установившегося режима и при этом обеспечить минимальную длительность переходного. Обычно эти требования противоречат друг другу, и при конструировании САУ приходится идти на компромисс между качеством работы в переходном и установившемся режимах. Указанные причины приводят к тому, что при оценке качества приходится отдельно определять качество управления в переходном и установившемся режимах и сопоставлять их друг с другом. Так как характер работы системы в разных режимах сильно отличается друг от друга, то и методики вычисления критериев качества оказываются различными. С этой точки зрения следует иметь в виду еще один фактор, связанный с характером поступающих на систему воздействий: способы вычисления ошибок управления различны для регулярных и случайных воздействий. В результате приходится излагать несколько способов расчета точности САУ в зависимости от режимов управления и характера воздействий.
2.2.2. Оценка качества переходного режима по переходной
характеристике Переходный режим вызван тем, что система инерционна и должна некоторое время приспосабливаться к поступающим на нее воздействиям. В этих условиях оценку качества удобно вести при наиболее тяжелом с точки зрения воспроизведения системой воздействии, таком, как ступенчатая функция А*l(t). Реакция системы на единичную ступенчатую функцию является переходным процессом h(t), по форме которого в простейшем случае и можно судить о качестве переходного режима.
На рис. 52. изображены переходные характеристики колебательного и монотонного типов, оценка которых проводится с помощью локальных критериев, называемых показателями качества переходной характеристики.

Рис. 52. Показатели качества переходной характеристики
Для характеристик колебательного типа обычно используются следующие показатели: Hm - перерегулирование, которое определяет относительное максимальное отклонение; время установления tу - момент достижения первого максимума; время регулирования tр, которое определяет длительность процесса по уровню + 0,05 относительно установившегося значения; период колебаний T.
Для монотонных характеристик наиболее употребительным является показатель длительности переходного процесса tр. В общем случае точное построение переходных характеристик и, следовательно, определение качества затруднительно. Существует ряд методов, позволяющих приближенно строить переходные характеристики, однако эти методы сложны и приводят к громоздким вычислительным работам. Найти точные значения указанных выше величин удается только для простейших систем первого и второго порядков. Для более сложных следящих систем существуют приближенные формулы их нахождения.
В основе формул лежит знание двух параметров: частоты среза разомкнутой следящей системы w с и запаса по фазе. Эти параметры могут быть найдены аналитически или по логарифмическим частотным характеристикам. Сводка вычислительных соотношений приводится в табл. П. 2.
2.2.3. Интегральный квадратичный критерий качества переходного режима
Локальные критерии качества обычно наглядны, но трудно вычисляются аналитически. Примером тому служат показатели переходной характеристики, рассмотренные выше. Интегральные критерии, особенно квадратичные, достаточно легко вычисляются, однако не так наглядны, как локальные. Обратимся к рис.53, на котором изображены два монотонных переходных процесса. Процесс 1 наименьшей длительности. Об этом может свидетельствовать такой косвенный фактор, как площадь между кривой h(t) и уровнем установившегося значения выходного процесса. Отсюда для оценки качества можно ввести критерий
![]()
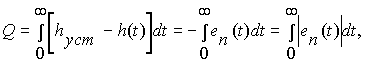
где через eп (t) обозначена ошибка переходного режима, представляющая разность между текущим и установившемся значениями переходной характеристики. Чем меньше Q, тем выше качество САУ.
Причем подынтегральная квадратичная функция потерь eп(t) будет неотрицательной как для монотонных, так и для колебательных процессов.
Очевидно, что описанные критерии можно использовать не только для случая переходной характеристики, но и при произвольных воздействиях.

Рис.53. Сравнение качества переходных характеристик
Рассмотрим методику нахождения интегрального квадратичного критерия переходного режима для регулярного воздействия x(t).
Изображение динамической ошибки можно записать в виде произведения
| e(p) = x(p)Kех(p) | (29) |
Не прибегая к нахождению оригинала eх(t), можно найти установившееся значение ошибки управления
![]() ,
,
или
![]() .
.
Если из полной ошибки eх(t) вычесть ошибку установившегося режима eх уст, то получим составляющую, которая равна ошибке переходного режима
еп(t) = eх (t) - eх уст.
Очевидно, что
еп(t) ![]() 0
при t
0
при t ![]()
![]() , так как eх
(t)
, так как eх
(t) ![]() eх уст.
eх уст.
Интегральный квадратичный критерий качества переходного режима определим как величину
![]()
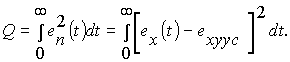
На основании известной теоремы Парсеваля, нахождение интегрального квадратичного критерия качества Q переходного режима сводится к вычислению интеграла Парсеваля
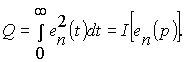 |
(30) |
Чтобы вычислить конкретное значение этого интеграла, функцию eп(p) записывают в виде отношения полиномов
 .
.
Тогда интеграл будет функцией параметров a , и b . Значения функций табулированы и для n < 4 приведены в табл. П.3.
Изображение ошибки переходного режима получаем из формулы:
![]()
где учтено, что изображение от постоянной ex уст равно e x уст /p.
Пример.
Найдем интегральный квадратичный критерий качества переходного процесса в системе управления антенной.
Передаточная функция разомкнутой системы
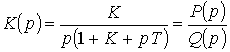 ,
,
Передаточная функция ошибки по задающему воздействию равна
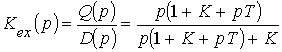 .
.
Так как рассматривается переходный процесс, то воздействием является единичная функция
x(t) = 1 (t)
с изображением
x(p)=1/p .
Изображение ошибки управления
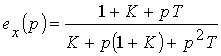 .
.
Установившееся значение ошибки
![]()
В итоге получим, что изображение ошибки переходного режима равно
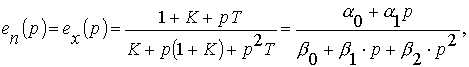
где
a 0 = 1+K; a 1 = T; b 0 = K; b 1 = 1+K; b 2 = T.
Согласно формуле (30) интегральный квадратичный критерий качества переходного режима равен интегралу Парсеваля
Q = I [e п (p)].
Используя данные табл. П.3. для n = 2, находим значение интеграла
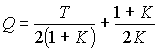 .
.
Из этого результата видно, что изменением параметров системы можно в широких пределах изменить величину критерия. Особенно характерны в этом отношении два параметра: R и T.
На практике для регулировки показателей переходного процесса широко используют коэффициент преобразования К элемента, не охваченного внутренней обратной связью. В то же время постоянную времени T усилителя следует подбирать так, чтобы величина первого слагаемого критерия не превышала допустимого уровня.
2.2.4. Системы управления при случайных воздействиях. Характеристики воздействий
На систему могут поступать как показные задающие воздействия, так и возмущающие, нарушающие нормальный ход управления. Воздействия могут быть неслучайными или случайными функциями времени.
Неслучайными, или регулярными, называются такие воздействия, закон изменения которых известен на всем интервале времени работы системы. Регулярные воздействия задаются функциями, например
X(t) = at; X(t) = bsinw t; u (t) = c e-xt и т.д.,
где все параметры a, b, c, l, w и т.п. считаются известными.
Регулярный характер воздействий не часто встречается на практике, так как предсказать заранее изменения переменных, особенно возмущающих воздействий, обычно невозможно. Тем не менее анализ качества при некоторых регулярных воздействиях, которые можно считать наиболее “тяжелыми”, позволяет дать оценку качества управления в наихудшем случае. В частности, такую оценку проводят для воздействий
x (t) = 1 (t)
типа единичных функций, полагая, что скачкообразное изменение воздействия определяет наиболее тяжелый режим работы САУ. Как уже известно, реакция на единичный импульс порождает переходную характеристику, поэтому оценка качества по переходной характеристике часто используется на практике. Как правило, предсказать ход изменения воздействий заранее нельзя. Наиболее ярким примером в этом отношении являются возмущающие воздействия. Так, в радиолокационных следящих системах часть возмущающих воздействий обусловлена наличием приемного устройства; описать закон изменения этих воздействий с помощью регулярных функций совершенно невозможно. В таких случаях наиболее подходящим аппаратом для описания воздействий являются случайные процессы. Свойства этих процессов носят вероятностный, или статистический, характер и изучаются в теории случайных процессов.
Использование случайных процессов в качестве моделей воздействий значительно расширяет возможности исследования систем автоматического управления. Это объясняется не только тем, что сами процессы удается описать более точно, но и тем, что появляется возможность оценивать качество управления с помощью небольшого числа величин для весьма разнообразных условий работы. Поэтому в настоящее время статистические методы исследования САУ играют основную роль в теории автоматического управления.
В самом общем случае воздействия могут состоять из суммы регулярных и случайных составляющих. Рассмотрим характеристики подобных процессов на примере задающего воздействия x(t). Итак, пусть x(t) является случайным процессом. Простейшей характеристикой случайного процесса считается математическое ожидание или среднее значение
mx(t) = <x (t) >.
Угловыми скобками здесь и далее обозначается операция нахождения математического ожидания (усреднения по множеству). Вычтем из исходного процесса его математическое ожидание и тогда получим случайную составляющую или центрированный случайный процесс
x0(t) = x (t) – mx(t) .
Математическое ожидание – это регулярная составляющая процесса x(t), а все статистические свойства процесса определяются его случайной составляющей x0(t) . Простейшей характеристикой случайной составляющей служит дисперсия
Dx (t) = < [x0 (t)]2 >.
При анализе стационарных систем будет рассматривать только стационарные случайные составляющие, у которых дисперсия Dx остается постоянной и от времени не зависит.
Величина, равная корню квадратного из дисперсии, называется среднеквадратическим (СКО) и обозначается
![]()
Размерность дисперсии равна квадрату
размерности процесса x0 (t), а размерность
СКО совпадает с размерностью процесса. Величина ![]() x
служит усредненной мерой оценки амплитуды случайной составляющей. Для
большинства случайных процессов вероятность превышения ими уровня 3
x
служит усредненной мерой оценки амплитуды случайной составляющей. Для
большинства случайных процессов вероятность превышения ими уровня 3![]() x
очень мала.
x
очень мала.
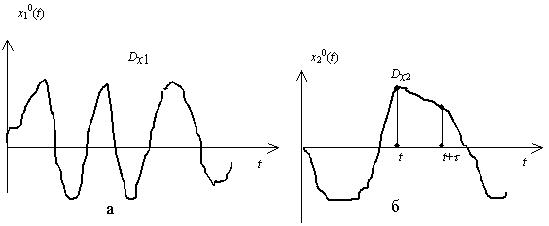
Рис. 54. Реализации случайных процессов
Дисперсия или СКО далеко не полностью определяют свойства случайной составляющей. Например, на риc. 54 а,б изображены реализации процессов с одинаковыми дисперсиями
Dx1 = Dx2 = Dx,
однако сразу видно, что свойства обоих процессов различны: скорость изменения первого процесса больше, чем второго. Для определения степени изменяемости случайного процесса вводят понятие корреляционной функции
Rx (t ) = < x0(t) x0 (t + t ) >
как среднего от произведения значений процесса в момент t и соседний с ним момент t + t (рис.54). Интервал t может быть положительным или отрицательным. Для стационарных случайных процессов, которые мы рассматриваем, корреляционная функция не зависит от выбора момента t, а является функцией только интервал t . Из рассмотрения рис. 54, а б понятно, что при одних и тех же t для “быстрых” процессов значение Rx( t ) будет меньше, чем для “медленных”, потому что степень зависимости между x0(t) и x0 (t + t ) у “быстрых” процессов меньше. Таким образом, для рассматриваемого примера
Rx1 (t ) £ Rx2 ( t ) .
В частном случае при
t = 0, Rx (0) = <[x0 (t)]2 > = Dx,
то есть значение корреляционной функции при нулевом аргументе равно дисперсии. Для нашего примера получим, что Rx1 (0) = Rx2 (0) = Dx. Примеры корреляционных функций для “быстрых” и “медленных” процессов при одинаковом значении дисперсий показаны на рис. 55. Отметим несколько свойств корреляционных функций стационарных случайных процессов:
Rx(t ) = Rx (-t ) - свойство четности;
Rx ( t ) <= Rx (0) – свойство невозрастания;
Rx( t )
![]() 0
при t
0
при t ![]()
![]() - асимптотические свойства.
- асимптотические свойства.

Рис.55. Корреляционные функции
Дополнительно заметим, что Rx( t ) может принимать и отрицательные значения.
Характеристику случайному процессу можно давать и в частотной области. Для этого используют понятие спектральной плотности Sx(w) . Она получается преобразованием Фурье от корреляционной функции:
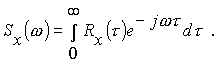
Обратное преобразование от спектральной плотности дает выражение корреляционной функции:
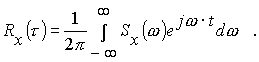
Из этого выражения легко получается соотношение между дисперсией и спектральной плотностью
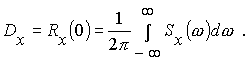
Спектральная плотность стационарных процессов обладает следующими свойствами:
Sx( w ) >= 0 - свойство неотрицательности;
Sx( w ) = Sx(-w ) - свойство четности;
Sx (w )
![]() 0 при w
0 при w
![]()
![]() - асимптотические свойства.
- асимптотические свойства.
“Быстрые” случайные процессы имеют более широкую спектральную плотность, чем “медленные”. На риc. 56. показаны спектральные плотности для того примера, который рассматривался выше.

Рис. 56. Спектральные плотности
Заметим, что из условия равенства дисперсий
Dx1 = Dx2
вытекает равенство площадей
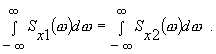
Перечисленные характеристики в дальнейшем используются при анализе качества управления.
2.2.5. Характеристики выходного случайного процесса. Стационарные формирующие фильтры
Предположим, что на вход стационарного линейного звена с импульсной характеристикой k(t) и частотной характеристикой
K(jw ) = K (t) e-jw t dt
поступает случайное воздействие
x(t) = mx (t) + x0 (t)
со стационарной случайной составляющей x0(t) и математическим ожиданием mx (t).
Найдем характеристики выходного процесса y(t) в установившемся режиме.
Благодаря принципу суперпозиции выходной процесс будет равен сумме
y(t) = my (t) + y0 (t).

Рис. 57. Преобразование случайного воздействия
Математическое ожидание выходного процесса my(t), то есть его регулярная составляющая, будет определяться только математическим ожиданием входного воздействия mx(t), а случайная составляющая y0(t) – только случайной составляющей x0(t). Способ нахождения выходного процесса при регулярном воздействии был нами уже рассмотрен в предыдущем подразделе, поэтому сосредоточим наше внимание на характеристиках преобразования случайной составляющей.
Пусть задана спектральная плотность Sx( w ) входного воздействия. Запишем окончательное выражение для спектральной плотности выходного процесса
Sy( w ) = Sx ( w ) K(jw )K(-jw ).
Учитывая, что произведение комплексно-сопряженных множителей равно квадрату модуля частотной характеристики или квадрату амплитудно-частотной, получим окончательную формулу для спектральной плотности
|
Sy(w ) = Sx(w ) ½ K(jw ) ½ 2 = Sx (w ) A2 (w ) |
(31) |
Таким образом, спектральная плотность выходного процесса определяется спектральной плотностью входного и частотной характеристикой звена.
Стационарное случайное воздействие
x0(t) со спектральной плотностью Sx(w
) можно представить как результат преобразования белого шума ![]() x(t)
с единичной спектральной плотностью
x(t)
с единичной спектральной плотностью
Nx = 1
звеном с частотной характеристикой Kф (jw ) (рис.58). Такое звено называется формирующим фильтром. Найдем частотную характеристику этого фильтра. Для этого разложим функцию спектральной плотности на два комплексно сопряженных множителя
Sx( w ) = Kx(jw ) Kx(-jw ).
Частотная характеристика формирующего фильтра равна прямому сомножителю этого разложения, то есть
Kф (jw ) = Rx (jw ) .
Докажем это. Согласно формуле (31) спектральная плотность выходного процесса формирующего фильтра (рис.58) равна произведению
Nx Kф (jw ) Kф (- jw ) .
Так как
Nx = 1, а Kф (jw ) = Kx(jw ),
то получим выходную спектральную плотность, равную произведению
Kx (jw ) K x ( - jw ) = Sx ( w ) ,
что и доказывает правильность выбора.
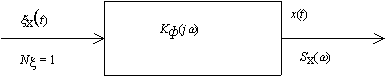
Рис. 58. Стационарный формирующий фильтр
Итак, чтобы найти частотную характеристику формирующего фильтра надо разложить спектральную плотность на комплексно-сопряженные множители и выбрать
Kф (jw ) = Kx (jw ).
Используя понятие формирующего
фильтра, преобразование воздействия x0(t) со спектральной
плотностью Sx( w ) можно представить как преобразование
белого шума ![]() x
( t) с единичной спектральной плотностью последовательно
соединенными формирующим фильтром и исходным звеном (рис.59).
x
( t) с единичной спектральной плотностью последовательно
соединенными формирующим фильтром и исходным звеном (рис.59).

Рис. 59. Преобразование воздействия с учетом формирующего фильтра
Такое представление упрощает процедуру вычислений.
Рассмотрим экспоненциальный случайный процесс со спектральной плотностью

Найдем частотную характеристику формирующего фильтра. Разложим спектральную плотность на комплексно-сопряженные множители:
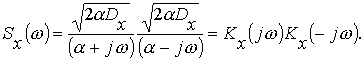
Частотная характеристика формирующего фильтра равна прямому множителю этого разложения
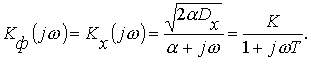
Формирующий фильтр в этом примере соответствует усилительному звену с коэффициентом преобразования
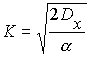
и апериодическому звену с постоянной времени T = 1/a.
2.2.6. Статистический анализ точности
Приведем анализ точности автоматических систем при случайных воздействиях, когда ошибка управления e(t) будет случайным процессом. Ограничимся рассмотрением того случая, когда случайные составляющие воздействия являются стационарными случайными процессами, а система работает в установившемся режиме.
Если случайная ошибка управления
e(t) = me(t) + e(t),
то есть состоит из суммы математического ожидания и случайной составляющей, критерий среднего значения квадрата ошибки управления имеет вид
Q = me (t) + De,
где De - дисперсия стационарной случайной составляющей ошибки e(t).
Для оценки точности требуется найти математическое ожидание me(t) ошибки управления и дисперсию De.
Методика нахождения регулярной составляющей ошибки (ошибки от регулярного воздействия) рассматривалась ранее.
Рассмотрим методику вычисления дисперсии ошибки De. Известно уравнение связи между дисперсией и спектральной плотностью ошибки
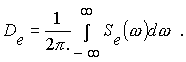
Таким образом, чтобы найти дисперсию ошибки надо определить спектральную плотность и вычислить интеграл. Рассмотрим случай, когда все воздействия, поступающие на систему, статистически независимы друг от друга. Спектральная плотность ошибки равна сумме спектральных плотностей от каждого из воздействий, т.е.
Se(w ) = Sex(w ) + Sev(w ).
Спектральная плотность ошибки от задающего воздействия
Sex(w ) = Sx(w ) Kex(jw ) Kex(-jw ),
а от возмущающего воздействия
Sev(w ) = Sv(w ) /Kev(jw ) Kev(-jw ).
Подставляя данные выражения в формулу для дисперсии ошибки, получим
De = Dex + Dev ,
то есть дисперсия ошибки при независимых воздействиях равна сумме дисперсии от каждого из воздействий в отдельности. Остается рассмотреть методику вычисления каждого слагаемого выражения. В качестве примера рассмотрим методику определения ошибки от задающего воздействия

Спектральную плотность воздействия мы представляли в виде произведения комплексно-сопряженных множителей
Sx(w ) = Kx(jw ) Kx(-jw ),
где Kx(jw ) - частотная характеристика формирующего фильтра.
Тогда дисперсия ошибки

Заменим переменную jw на p, а дифференциал dw =dp/j . После этого
интеграл примет следующий вид:
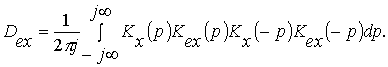
Данное выражение является интегралом Парсеваля от произведений функций Kx(p)Kex(p). Таким образом, дисперсия ошибки управления может быть представлена в виде интеграла Парсеваля от произведения передаточной функции формирующего фильтра на передаточную функцию ошибки
Dex = I [Kx(p) Kex(p)].
Значение интеграла Парсеваля находится по табл. П.3, для чего произведение записывают в виде отношения полиномов.
Таким же способом определяются дисперсии ошибок от возмущающих воздействий
Dev = I[Kv(p) Kev(p)].
В частном случае, если воздействие будет белым шумом со спектральной плотностью Nv, вычисление дисперсии ошибки проводится по формуле
Dev = Nv I [Kev(p)].
На рис. 60 изображены:
АЧХ замкнутой следящей системы Ayx(w ); квадрат
этой функции ![]() спектральная
плотность возмущающего воздействия Sv(w ) и график произведения
А2yx(w )Sv(w ) (т.к.
частотная характеристика ошибки от возмущающего воздействия с обратным знаком
совпадает с частотной характеристикой замкнутой системы).
спектральная
плотность возмущающего воздействия Sv(w ) и график произведения
А2yx(w )Sv(w ) (т.к.
частотная характеристика ошибки от возмущающего воздействия с обратным знаком
совпадает с частотной характеристикой замкнутой системы).

Рис.60. Спектральная плотность ошибки от возмущающего воздействия
Дисперсия ошибки пропорциональна площади под кривой Sv(w )A2yx(w ). При этом очевидно, что чем шире функция Ayx(w ), тем больше будет площадь и тем больше дисперсия ошибки. Иначе говоря, расширение полосы пропускания замкнутой следящей системы приводит к увеличению дисперсии ошибки от возмущающего воздействия. Амплитудно-частотная характеристика Aex(w ) и квадрат этой функции показаны на рис.61.

Рис.61. Спектральная плотность ошибки от задающего воздействия
Спектр задающего воздействия Sx(w ) узкополосный, и его положение также показано на рисунке.
Чем шире полоса пропускания системы, тем в большем диапазоне функция Aex(w ) будет близкой к нулю, тем меньше будет площадь под кривой Sx(w )Aex(w ) и тем меньше будет дисперсия ошибки. Таким образом, ширина полосы пропускания системы различным образом влияет на величину дисперсии ошибок. Расширение полосы уменьшает дисперсию от задающего воздействия, но увеличивает от возмущающего воздействия, приложенного на входе.
2.2.7. Параметрическая оптимизация
Если структура системы определена, то значение критерия качества будет зависеть от значений ее параметров. Под параметрами системы будем понимать такие величины, как коэффициенты преобразования, постоянные времени и т.п. отдельных ее звеньев. Обозначим эти параметры через
g = g 1, g 2, g 3, ... g r .
Тогда критерий будет функцией
Q(g 1,g 2, ..., g r) = Q(g ),
где число r определяет количество параметров, которые мы можем изменять. Как правило, влияние параметров на величину Q неоднозначно. При некоторых значениях
g = g опт
эта величина может принимать экстремальное значение Qэкс. Если характер экстремума согласуется с целью управления, то параметры, при которых он достигается, называются оптимальными. Например, при оценке точности системы по критерию минимума среднего значения функции потерь оптимальными будут те параметры, при которых величина Q достигает своего минимума
Qэкс = minQ .
Определение оптимальных параметров называется задачей параметрической оптимизации, которая относится к классу вариационных задач. При определении оптимальных параметров обычно приходится сталкиваться с ограничениями, накладываемыми на условия выбора. Простейшим примером таких ограничений может служить требование положительности постоянных времени звеньев. В противном случае задача может потерять физический смысл. При иных условиях могут накладываться ограничения на диапазон выбираемых параметров.
В общем виде ограничения носят характер неравенств
F1(g ) < N1; F2 (g ) < M2, ..., Fm (g ) < Mm,
где Fi(g ) - некоторые функции от параметров.
Решение задачи параметрической оптимизации с учетом ограничений производится методами математического программирования. Выбор каждого конкретного метода зависит от вида функций Q(g ) и Fi(g ). Если эти функции линейные относительно параметров y, решение ведется методами линейного программирования. Все остальные задачи решаются методами нелинейного программирования. Среди них следует выделить классические методы определения экстремума, градиентные методы, динамическое программирование.
Методы математического программирования являются алгоритмическими. Они не предназначены для получения результатов в явном виде, а дают лишь алгоритмы решения, с помощью которых численными методами могут быть получены искомые оптимальные параметры. Решение в явном виде имеет место лишь в простейших частных случаях.
Если ограничения на выбираемые параметры не накладываются, то для отыскания минимума функции Q(g ) используются необходимые условия существования экстремума.
Пример.
Рассмотрим угломерную следящую систему, передаточная функция которой в разомкнутом состоянии имеет вид K(p)=K/p.
Пусть задающее воздействие x(t) будет экспоненциально коррелированным стационарным случайным процессом со спектральной плотностью
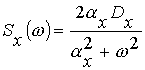 .
.
Учтем только возмущающее воздействие v(t) от шумов приемника со спектральной плотностью
Sv (w ) = Nv .
Найдем оптимальное значение коэффициента преобразования САУ, обеспечивающее минимум дисперсии ошибки слежения в установившемся режиме.
При статистически независимых воздействиях
De = Dex + Dev .
Определим дисперсию ошибки от задающего воздействия
Dex = I[Kx(p) Kex(p)],
где Kex(p) - передаточная функция ошибки по задающему воздействию;
Kx(p) - передаточная функция стационарного формирующего фильтра.
Дисперсия ошибки от задающего воздействия
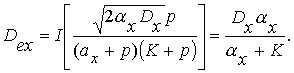
Дисперсия от возмущающего воздействия
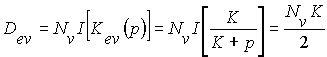 .
.
Суммарная дисперсия

В данной задаче имеется только один оптимизируемый параметр g = K.
Оптимальное значение параметра определим графическим способом.
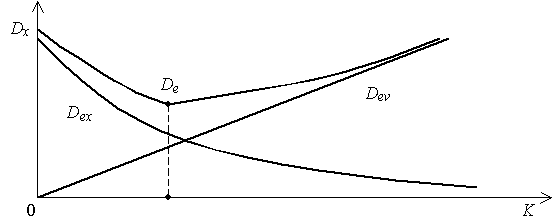
Рис. 62 Дисперсия ошибки в угломерной системе
Это значение соответствует минимуму Q.
При параметрической оптимизации часто используют численные методы, основанные на различных методах поиска экстремума.