
Рассмотрим системы автоматического управления, в которых передача, обработка и преобразование информации осуществляются только в определенные моменты времени, то есть дискретно. В этом случае в системах действуют сигналы, являющиеся некоторой последовательностью импульсов, и такие системы называются дискретными. Создание дискретных систем может быть вызвано многими причинами.
Во-первых, принцип действия некоторых элементов, входящих в систему, может быть дискретным. К примеру, в системе управления ракетой имеется импульсная радиолокационная станция (РЛС), измеряющая координаты цели и ракеты (рис. 1.1). По своему принципу действия она выдает информацию дискретно с частотой следования импульсов станции, поэтому и вся система управления будет дискретной. В качестве другого примера можно указать на САУ, имеющие в своем составе цифровые вычислительные машины (ЦВМ), являющиеся дискретными устройствами.

Рис. 1.1. Блок - схема системы автоматического управления
Во-вторых, в дискретных системах проще реализовать сложные алгоритмы управления. Так, при использовании ЦВМ алгоритм задается в виде программы, сложность которой практически не влияет на конструкцию системы. Смена программы, то есть алгоритма управления, производится без больших затрат времени. В непрерывных же САУ повышение сложности алгоритма управления требует включения в состав системы новых элементов, а замена алгоритма связана с существенным усложнением конструкции.
В-третьих, точность решения алгоритмов управления с помощью дискретных устройств (например, ЦВМ) обычно выше, чем с помощью непрерывных. Это положение требует более подробного объяснения. Дискретная обработка информации за счет импульсного характера сигналов неизбежно приводит к ее потере, так как на интервалах, где импульсы отсутствуют, полезная информация не используется. Поэтому, если для решения одного и того же алгоритма использовать дискретные и непрерывные устройства, то точность последних в идеальном случае будет выше. За счет потери части информации дискретные устройства обладают методической погрешностью, то есть такой, которая зависит от метода обработки. Однако как дискретные, так и непрерывные устройства имеют и другие погрешности - инструментальные, зависящие от неточностей изготовления отдельных элементов, нестабильностей параметров, внутренних шумов и помех. Оказывается, что инструментальные погрешности непрерывных устройств значительно больше, чем устройств дискретных, и сильно растут с усложнением алгоритма обработки. В итоге суммарная погрешность дискретных устройств оказывается меньше инструментальной погрешности непрерывных, что и позволяет говорить о более высокой точности работы дискретных систем.
Перечисленные преимущества привели к широкому использованию дискретных систем. Особенно большое распространение получили системы с ЦВМ. Классификация дискретных систем базируется на признаках, определяющих особенности протекания процессов управления и методики исследования. По этим признакам дискретные системы можно разделить на линейные и нелинейные (в зависимости от применимости к ним принципа суперпозиции) и на стационарные и нестационарные (по степени изменения параметров во времени). Кроме них имеются и другие признаки, характерные только для дискретных систем. Перечислим их и дадим дополнительную классификацию дискретных САУ.
При изучении теории дискретных систем следует четко различать такие понятия, как процесс и сигнал. Процесс отображает ту информацию, которая преобразуется системой, а сигнал является физическим носителем этой информации. В непрерывных системах оба эти понятия отождествляются, так как значения сигнала в любой момент времени пропорциональны значениям процесса. В теории дискретных систем указанные понятия надо различать. Благодаря наличию импульсных сигналов информация в системе передается отдельными частями, квантами. Процессы, описывающие преобразование этой информации, называются дискретными, а преобразование непрерывных процессов в дискретные называется квантованием. Существует три вида квантования: по времени, по уровню и по времени и уровню одновременно. При квантовании по времени исходная непрерывная функция x(t) преобразуется в последовательность дискретных значений x(ti), где ti-это дискретные моменты времени на временной оси. Расстояние между значениями ti может быть произвольным, однако на практике чаще всего имеет место случай периодического квантования с постоянным периодом повторения Тn, показанный на рис.1.2, а. При этом ti =iTn, где число i может принимать все целые значения от -∞ до +∞. При квантовании по уровню вся область возможных х разбивается на отдельные дискретные уровни и дискретный процесс может принимать только те значения, которые совпадают с выбранными уровнями. На рис.1.2, б показано квантование по уровню процесса x(t) в случае постоянного шага квантования Δ. Комбинированный случай квантования по времени и уровню при постоянном периоде Tn и шаге Δ показан на рис.1.2, в. Информация о значениях дискретного процесса передается с помощью импульсных сигналов путем модуляции их параметров: амплитуды, длительности, фазы, частоты. Отсюда различают системы с амплитудной, широтной, фазовой и частотной модуляциями. Особую группу составляют системы с кодовой модуляцией, когда значения процесса передаются путем выбора числа импульсов и их местоположения в группе. Сразу заметим, что такой вид модуляции применяется в цифровых вычислительных машинах. В некоторых дискретных системах вид модуляции и форма используемых импульсов могут влиять на качество обработки информации, что усложняет методику исследования. Одним из достоинств кодовой модуляции является то, что форма импульсов и тип кода практически не влияют на работу системы.

Рис. 1.2. Квантование сигналов по времени (а); уровню (б); по времени и по уровню (в)
Если каждый квант информации дискретного процесса, квантованного только по времени, передается с помощью импульса при определенном виде модуляции его параметров, то дискретные системы называются импульсными. В итоге различают импульсные системы с амплитудной (АИМ), широтной (ШИМ), фазовой (ФИМ), частотной (ЧИМ) видами модуляции. Кроме того, бывают системы с комбинированными видами модуляции. Если в системах с АИМ амплитуда импульсов пропорциональна значениям квантованного процесса, то такие импульсные системы могут быть линейными. При всех других видах модуляции они относятся к классу нелинейных систем.
Если в дискретных САУ преобразуются процессы, квантованные по уровню, то они называются релейными. Системы с квантованием процессов по времени и уровню называются цифровыми. Как релейные, так и цифровые системы являются нелинейными. Если все сигналы в системе являются дискретными, то она называется чисто дискретной, если же часть сигналов остается непрерывными, то дискретно-непрерывной. Так как в чисто дискретной системе все сигналы и, следовательно, процессы имеют одинаковую дискретную структуру, то теория таких систем сравнительно проще. Дискретно-непрерывные системы являются промежуточным случаем между непрерывными и чисто дискретными, поэтому методика их исследования сложнее, так как она должна включать в себя элементы теории как непрерывных, так и чисто дискретных систем. Исходя из этого, целесообразно теорию дискретных систем начинать с изучения систем чисто дискретных, распространив затем полученные результаты на дискретно-непрерывные. Чтобы не усложнять терминологию, чисто дискретные системы в дальнейшем будем называть просто дискретными. Там, где это необходимо по ходу описания, будет применяться полный термин "чисто дискретная система". В развитие теории дискретных систем большой вклад внесли советские ученые Я. 3. Ципкин [16], Л. Т. Кузин [10] и целый ряд других.
В процессе изложения дальнейшего материала мы не будем касаться вопросов теории релейных систем, а также импульсных систем с ШИМ, ФИМ и ЧИМ. Основные сведения по этим системам можно найти в указанной выше литературе. Таким образом, мы сосредоточим наше внимание на цифровых системах и импульсных с амплитудно-импульсной модуляцией. С точки зрения видов квантования, показанных на рис. 1.2, будем рассматривать только процессы с квантованием по времени и по времени и уровню одновременно (рис. 1.2, а и б).
В дискретных системах осуществляется преобразование информации, заданной в виде дискретных процессов, квантованных по времени или по времени и уровню одновременно. Введем специальные обозначения для этих процессов. Исходные непрерывные процессы, из которых получаются дискретные, называются огибающими и обозначаются обычными символами, например x(t).
Соответствующие им дискретные процессы с квантованием по времени (рис. 1.2, а) и постоянным периодом Tn, обозначают через x(iTn), имея в виду, что i может быть любым целым числом. Чтобы получить дискретный процесс, квантованный по времени, по заданной огибающей достаточно в функции x(t) положить значение t = iTn, то есть
x(iTn) = x(t = iTn).
Дискретный процесс, квантованный по времени с постоянным периодом Tn и по уровню с постоянным шагом Δ, будем обозначать символом х(iTn) (рис. 1.2, б). Получить его по заданной функции огибающей можно по формуле

где F обозначает операцию нахождения ближайшего к значению х(iТn) числа с шагом квантования по уровню Δ. Операция F является нелинейной, поэтому цифровые системы с квантованием процессов по времени и уровню относятся к классу нелинейных. Их особенности мы будем рассматривать отдельно в дальнейшем, а сейчас остановимся на линейных дискретных системах с процессами х(iТn), квантованными по времени.
 |
 |
| Рис. 1.3. Изображение дискретной системы | Рис. 1.4. Неоднозначность дискретной функции |
Работа дискретной системы сводится к преобразованию входных процессов x(iTn) в выходные у(iТn) с некоторыми заданными условиями. Схематически это отображено на рис. 1.3. По характеру желаемого преобразования дискретные системы подразделяются на те же классы, что и непрерывные, то есть на следящие, стабилизирующие, интегрирующие и др., однако возможности преобразования процессов в них имеют свои характерные особенности, которые мы и рассмотрим. Главной особенностью дискретных процессов x(iTn) является их неоднозначность. Заключается она в том, что одним и тем же дискретным процессам может соответствовать множество различных огибающих. Для примера на рис. 1.4 показаны две функции x1(t) и x2(t), которым соответствует один и тот же процесс х(iТn). Неоднозначность дискретных функций, в частности выходного процесса у(iТn) системы (рис. 1.3), может привести к неправильным выводам по результатам работы системы, поэтому предварительно должны быть изучены те условия, при которых возникающая неоднозначность была бы сведена к минимуму. Возникновение неоднозначности является следствием потери информации на интервалах между моментами квантования. Рассмотрим подробнее, как это происходит. Пусть квантованию с периодом Tn и частотой
| Ω = | 2π
Tn |
подвергается гармонический процесс х(t) = a cos ωt.
Найдем зависимость между частотой исходного процесса и частотой огибающей ω0 квантованного процесса х(iTn). Первоначально положим, что частота ω << Ω. Квантованный сигнал для этого случая показан на рис. 1.5, а. Так как в полупериод исходного процесса x(t) укладывается большое число дискретных значений x(iTn), то по ним наблюдателю легко получить значение частоты огибающей, которая будет совпадать с частотой исходного процесса. Таким образом, при малой частоте неоднозначности в ее оценке по дискретным данным не будет. Если построить зависимость ω0 от ω (рис. 1.6), то при ω << Ω она будет линейной.

Рис. 1.5. Квантование гармонического сигнала

Рис. 1.6. Стробоскопический эффект
Предельным случаем для правильной оценки частоты ω будет тот, когда на каждом полупериоде окажется одно значение x(iTn). Этот случай изображен на рис. 1.5, б, и он соответствует частоте
| ω = | Ω
2 |
При ω >  на каждый полупериод будет
приходиться меньше одного значения x(iTn), что приведет к
неоднозначности в определении ω. Так, если взять ω = Ω, то частота огибающей
выходного процесса, как это видно из рис. 1.5, в, будет равна ω0 = 0,
это и показано на рис. 1.6.
на каждый полупериод будет
приходиться меньше одного значения x(iTn), что приведет к
неоднозначности в определении ω. Так, если взять ω = Ω, то частота огибающей
выходного процесса, как это видно из рис. 1.5, в, будет равна ω0 = 0,
это и показано на рис. 1.6.
При ω = 3Ω/2 (рис. 1.5, г) мы получим дискретный процесс, совпадающий с
x(iTn) при ω =  (рис. 1.5, б). Подобные
рассуждения можно продолжить и показать, что оценка частоты ω исходного процесса
по частоте огибающей ω0 дискретного процесса будет неоднозначной.
График этой зависимости изображен на рис. 1.6. Однозначность сохраняется лишь в
диапазоне
(рис. 1.5, б). Подобные
рассуждения можно продолжить и показать, что оценка частоты ω исходного процесса
по частоте огибающей ω0 дискретного процесса будет неоднозначной.
График этой зависимости изображен на рис. 1.6. Однозначность сохраняется лишь в
диапазоне
| 0 < ω < | Ω
2 |
Описанное свойство называется стробоскопическим эффектом и является важнейшей особенностью дискретных систем. Из него следует важный для практики создания дискретных систем вывод: чтобы дискретная система была работоспособной и ее выходные данные имели однозначную интерпретацию, частоту квантования следует выбирать из условия Ω > 2ωгр, где ωгр - максимальная частота спектра входного сообщения. Впервые это условие в более широкой постановке в виде теоремы было получено в 1933 году академиком В. А. Котельниковым. Теорема Котельникова устанавливает минимальное допустимое значение частоты квантования Ω или максимальный период дискретности Tn, обеспечивающие преобразование информации без больших потерь при квантовании по времени.
Перейдем к математическому описанию линейных дискретных систем с помощью так называемых разностных уравнений. По своей структуре эти уравнения во многом напоминают дифференциальные уравнения непрерывных систем. Чтобы эта аналогия была более полной, рассмотрим вначале понятия о конечных разностях, для чего изобразим на рис. 1.7 дискретную функцию х(iТn). Нулевой конечной разностью называется само значение дискретной функции и обозначается через
Δ0 x(iTn) = x(iTn)
Это понятие аналогично нулевой производной непрерывной функции.
Первой конечной разностью называется выражение
Δ1 x(iTn) = (iTn) - x[(i-1)Tn], (1.1)
где x[(i-1)Tn] - значение функции в предшествующем периоде следования (рис. 1.7). Δ1 x(iTn) определяет приращение функции на период и по смыслу близко к понятию первой производной непрерывных функций.

Рис. 1.7. Определение конечных разностей
Вторая разность равна разности первых разностей:
Δ2 x(iTn) = Δ1 - Δ1 x[(i-1)Tn] = x(iTn)-2x[(i-1)Tn]+ x[(i-2)Tn]. (1.2)
Третья разность равна разности вторых разностей:
Δ3 x(iTn) = Δ2 x(iTn) -
Δ2 x[(i-1)Tn] =
= x(iTn) -
3x[(i-1)Tn] + 3x[(i-2)Tn] - 3x[(i-2)Tn]-
x[(i-3)Tn],
и, в общем случае, разность k-го порядка
Δk x(iTn) = Δk-1 x(iTn) - Δk-1 x[(i-1)Tn], (1.3)
Этой разности можно сопоставить понятие k-й производной непрерывной функции. k-ю разность можно выразить через значения дискретной функции следующим образом:
Δk x(iTn) = x(iTn) -
kx[(i-1)Tn] + C2k x[(i-2)Tn] -
C3k x[(i-3)Tn] +
+ ... -
Ck-1k x[(i-k+1)Tn] + x[(i-k)Tn],
(1.4)
где Сrk - число сочетаний из k по r.
Разностное уравнение дискретной системы устанавливает соответствие между входным и выходным дискретными процессами и их разностями. Линейным системам соответствует линейное соотношение между этими переменными, которое имеет вид:
| ^ C0 |
y (iTn) + | ^ C1 |
Δ1 y(iTn) + ... + | ^ Cn |
Δn y(iTn) = | ^ b0 |
x (iTn) + ... + | ^ bm |
Δm x(iTn) | (1.5) |
Уравнение (1.5) называется линейным конечно-разностным уравнением и по своей
структуре соответствует линейному дифференциальному уравнению (1.4).
Коэффициенты  и
и
 определяются
параметрами системы, в том числе они зависят от периода повторения
Tn. Если параметры системы не зависят от времени, то коэффициенты
уравнения (1.5) будут постоянными и система называется стационарной. В
дальнейшем, впредь до особых оговорок, займемся изучением только стационарных
систем. Максимальный порядок п разности выходного процесса называется порядком
уравнения или порядком дискретной системы.
определяются
параметрами системы, в том числе они зависят от периода повторения
Tn. Если параметры системы не зависят от времени, то коэффициенты
уравнения (1.5) будут постоянными и система называется стационарной. В
дальнейшем, впредь до особых оговорок, займемся изучением только стационарных
систем. Максимальный порядок п разности выходного процесса называется порядком
уравнения или порядком дискретной системы.
Решение разностного уравнения можно записать в виде суммы
y(iTn) = yn(iTn)+ yx(iTn), (1.6)
которая состоит из дискретного переходного процесса yn(iTn) и вынужденного процесса yx(iTn). Переходный процесс находится из решения однородного уравнения
| ^ C0 |
yn(iTn) + | ^ C1 |
Δ1yn(iTn) + ... + | ^ Cn |
Δnyn(iTn) = 0 | (1.7) |
при начальных условиях у(0), Δ1 y(0), ... , Δn-1 y(0) для момента включения системы t = 0. Вынужденный процесс yx(iTn) является частным решением уравнения (1.5) при нулевых начальных условиях и заданном воздействии х(iTn).
Таким образом, как с точки зрения структуры уравнений, так и с точки зрения характера решения линейные дифференциальные и конечно-разностные уравнения имеют много общего, что и приводит ко многим аналогиям в методиках исследования непрерывных и дискретных систем. Линейное разностное уравнение можно представить и в другой форме записи, для чего в уравнении (1.5) надо раскрыть конечные разности по формуле (1.4) и сгруппировать все слагаемые с общими множителями вида у[(i-k)Tn] и х[(i-r)Тn], где число k будет иметь значения 0, 1, 2, ..., n, а число r значения 0, 1, 2, ..., m. После группировки уравнение примет следующий вид:
c0 y(iTn) + c1 y[(i-1)Tn]
+ ... + cny[(i-n)Tn] =
= b0
x(Tn)+ b1 x[(i-1)Tn] + ... + bm
x[(i-m)Tn], (1.8)
где коэффициенты с и b определяются коэффициентами  и
и  уравнения (1.5). В уравнение (1.8)
вошли входная и выходная переменные с учетом их запаздывания на конечное число
периодов. Уравнения такого вида называются разностными в рекуррентной форме
записи. Для объяснения такого названия выразим из уравнения (1.8) значение
выходной переменной
уравнения (1.5). В уравнение (1.8)
вошли входная и выходная переменные с учетом их запаздывания на конечное число
периодов. Уравнения такого вида называются разностными в рекуррентной форме
записи. Для объяснения такого названия выразим из уравнения (1.8) значение
выходной переменной
| y(iTn) = | 1
C0 |
{b0x(iTn) + b1x[(i-1)Tn] + ... + bm x[(i-m)Tn]} - |
| - c1 y[(i-1)Tn]- c2 y[(i-2)Tn] - ... - cn y[(i-n)Tn]. | ||
Очевидно, что полученную формулу можно рассматривать как алгоритм вычисления выходной переменной по значениям входной переменной в m предшествующих моментах времени и (n-1) значениям выходной переменной, найденным на предыдущих этапах вычислений. Такая методика носит название рекуррентной, откуда и следует название уравнения.
Так как уравнения (1.5) и (1.8) по своему содержанию подобны, то решение рекуррентного уравнения полностью совпадает с решением (1.6) конечно-разностного уравнения. При этом переходный процесс находится из решения однородного уравнения
c0 yn(iTn) + c1 yn[(i-1)Tn] + ... + cn yn[(i-n)Tn] = 0 (1.9)
с начальными условиями y(0), у(-Тn), у(-2Tn), ... , у[-(n-1)Tn]. Вынужденный процесс является решением уравнения (1.8) при нулевых начальных условиях и заданной функции x(iTn). Для исследования дискретных систем используются обе формы записи разностного уравнения в зависимости от конкретных решаемых задач.
Пример 1.1.
Предположим, что дискретная система описывается конечно-разностным уравнением второго порядка
| ^ C0 |
y(iTn) + | ^ C1 |
Δ1 y(iTn) + | ^ C2 |
Δ2 y(iTn) = | ^ b0 |
x(iTn). |
Составим уравнение в рекуррентной форме, для чего воспользуемся выражениями конечных разностей (1.1) и (1.2). Левая часть уравнения запишется в виде
| ^ C0 |
y (iTn)+ | ^ C1 |
{y (iTn) - y[(i-1)Tn]} + | ^ C2 |
{ y (iTn) - 2y[(i-1)Tn] + y[(i-2)Tn]} = |
| = ( | ^ C0 |
+ | ^ C1 |
+ | ^ C2 |
) y (iTn) - ( | ^ C1 |
+ 2 | ^ C2 |
y [(i-1)Tn] + | ^ C2 |
y [(i-2)Tn]. |
Обозначая
| C0 = ( | ^ C0 |
+ | ^ C1 |
+ | ^ C2 |
); C1 = ( - | ^ C1 |
- 2 | ^ C2 |
); C2 = | ^ C2 |
; b2 = | ^ b2 |
получаем уравнение второго порядка в рекуррентной форме
C0 y(iTn)+ C1 y[(i-1)Tn]+ C2 y[(i-2)Tn] = b0(iTn).
Выразим в явном виде значение выходной переменной
| y(iTn) = | 1
C0 |
{b0 x(iTn) - C1 y[(i-1)Tn]- C2 y[(i-1)Tn]}. |
Пусть огибающая входного процесса является линейной функцией
x(t) = t,
тогда дискретная функция равна
x(iTn) = iTn.
Найдем несколько значений выходного процесса при нулевых начальных условиях
у(0) = 0; y(-Tn) = 0.
Полагая i = 1, находим значение выходной переменной на первом шаге
| y(Tn) = | 1
C0 |
{b0 x(Tn) - C1 y(0)] = | b0
C0 |
Tn |
Взяв i = 2, находим значение на втором шаге
| y(2Tn) = | 1
C0 |
{b0 x(2Tn) - C1 y(Tn) - C2 y(0)] = |
| = | 1
C0 |
{b0 2Tn - C1 | b0
C0 |
Tn) = | b0
C0 |
( 2 - | C1
C0 |
) Tn. |
По такой же схеме можно последовательно вычислять значения выходной переменной и в другие моменты времени.
Одним из наиболее распространенных методов анализа линейных дискретных систем является операторный метод, основанный на дискретном преобразовании Лапласа, которое по своим возможностям и методике применения близко к преобразованию Лапласа для непрерывных функций.
Дискретным преобразованием Лапласа (ДПЛ) от функции х(iTn) называется сумма
| x*(p) = | ∞ Σ i = 0 |
x(iTn) e-piTn = D[x(iTn)], (1.10) |
где р - комплексная переменная. Легко увидеть аналогию между этим соотношением и непрерывным преобразованием Лапласа L[x(t)]. Верхний индекс в виде звездочки у изображения х*(р) поставлен, чтобы отличать его от изображения непрерывной функции х(р).
Рассмотрим основные свойства дискретного преобразования Лапласа, которые будут использоваться при дальнейшем изложении.
а) ДПЛ обладает свойством периодичности, заключающемся в том, что
х*(р) = x*(p + jkΩ), (1.11)
где Ω = 2π / Tn - частота квантования, k - любое целое число (нуль, положительное или отрицательное). Докажем это свойство, для чего согласно (1.10) запишем сумму
| x*(p + jkΩ) = | ∞ Σ i = 0 |
x(iTn) e-(p + jkΩ)iTn = | ∞ Σ i = 0 |
x(iTn) e-pTn e-jki Ω Tn |
Так как ΩTn = 2π, то сомножитель
e-jki Ω Tn = e-j 2ki π = e-j 2 π = 1
поскольку произведение целых чисел ki, в свою очередь, дает целое число. Таким образом, получаем
| x*(p + jkΩ) = | ∞ Σ i = 0 |
x(iTn) e-piTn = x*(p), |
что и требовалось доказать.
Свойство периодичности говорит о том, что функция х*(р) располагается на комплексной плоскости р периодически относительно мнимой оси Im p с периодом jΩ (рис. 1.8).

Рис. 1.8. Главная полоса комплексной плоскости
Для изучения функции х*(р) достаточно рассматривать лишь главную полосу в пределах
- j  ≤ Im p ≤ j
≤ Im p ≤ j 
(рис. 1.8), поэтому обратное дискретное преобразование Лапласа
| x(iTn) = | Tn
2 π j |
j  ∫ -j  |
x*(p) epiTn dp = D-1[x*(p)] (1.12) |
имеет область интегрирования только в пределах главной полосы.
б) Связь между изображением х*(р) дискретной функции и изображением х(р) непрерывной огибающей имеет вид
| x*(p) = | 1
Tn |
∞ Σ k = -∞ |
x(p - jkΩ). (1.13) |
Докажем это соотношение, для чего предварительно рассмотрим некоторые свойства бесконечной периодической последовательности дельта-функций, следующих с периодом Tn
| Δ(t) = | ∞ Σ i = -∞ |
δ(t - iTn). |
Как и всякую периодическую функцию ее можно разложить в ряд Фурье и представить в виде бесконечной суммы гармонических составляющих
| Δ(t) = | ∞ Σ k = -∞ |
ck ejk Ω t, (1.14) |
где комплексная амплитуда k-й гармоники
| ck = | 1
Tn |
Tn
2 ∫ -Tn 2 |
Δ(t) ejk Ω t dt = | 1
Tn |
Tn
2 ∫ -Tn 2 |
∞ Σ i = -∞ |
δ(t - iTn) ejk Ω t dt. |
Так как интегрирование ведется в пределах
| - | Tn
2 |
≤ t ≤ | Tn
2 |
, |
то из всей последовательности дельта-функций в этот предел попадает лишь центральное слагаемое при i = 0, а поэтому
| ck = | 1
Tn |
Tn
2 ∫ -Tn 2 |
δ(t - iTn) ejk Ω t dt = | 1
Tn |
. |
Подставляя это равенство в формулу (1.14), получаем ряд Фурье в виде
| Δ (t) = | 1
Tn |
∞ Σ k = -∞ |
ejk Ω t | . |
Теперь найдем, чему равен интеграл от произведения функций:
| ∞ ∫ 0 |
Δ (t) e-pt dt = | ∞ ∫ 0 |
∞ Σ i = -∞ |
δ(t - iTn) x(t) e-pt dt = |
| = | ∞ Σ i = 0 |
∞ ∫ 0 |
δ(t - iTn) x(t) e-pt dt = | ∞ Σ i = -∞ |
x(iTn) e-piTn = x*(p). (1.15) |
Здесь при замене местами суммирования и интегрирования нижний предел суммирования принят равным нулю, так как функция x(t) берется в пределах от нуля до бесконечности. Выражение (1.15) дает связь между изображением дискретной функции х*(р) и непрерывной огибающей x(t). Подставим в это выражение вместо Δ (t) ее разложение в виде ряда Фурье и получим
| x*(p) = | ∞ ∫ 0 |
Δ(t) x(t) e-pt dt = | ∞ ∫ 0 |
1
Tn |
∞ Σ k = -∞ |
ejk Ω t x(t) e-pt dt = |
| = | 1
Tn |
∞ Σ k = -∞ |
∞ ∫ 0 |
x(t) e- (p - jk Ω) t dt. |
Внутренний интеграл является преобразованием Лапласа от x(t) с комплексной переменной р - jkΩ, что приводит к формуле (1.13).
Для практического использования ДПЛ удобно ввести новую ком-плексную переменную z = epTn.
Получающееся при этом выражение
| х*(z) = | ∞ Σ i = 0 |
x(iTn) z-1 = Z[x(iTn)] (1.16) |
называется z - преобразованием. Рассмотрим соответствующее ему обратное преобразование, для чего в формуле (1.12) введем новые обозначения:
| e-piTn = zi; dz = Tn epTn dp; dp = | 1
Tn |
z-1 dz. |
Так как комплексная переменная p меняется в пределах
| - j | Ω
2 |
≤ p ≤ j | Ω
2 |
, |
то новая переменная z будет находиться в диапазоне
| e | - j Ω
2 |
≤ z ≤ e | j Ω
2 |
. |
В этих пределах модуль |z| = 1, а аргумент
- π ≤ arg z ≤ π,
поэтому интегрирование в плоскости z будет идти вдоль окружности единичного радиуса. После всех подстановок получим формулу обратного z-преобразования
| x(iTn) = | 1
2 π j |
 |x|=1 |
x*(z) zi-1 dz, |
где символически обозначен путь интегрирования вдоль окружности еди-ничного радиуса. Продолжим изучение свойств ДПЛ уже в форме z-преобразования.
в) Изображение функции х[(i- k)Tn] с запаздывающим аргументом kTn равно
Z{x[(i- k)Tn]} = z-kx*(z). (1.17)
Для доказательства запишем z-преобразование от рассматриваемой функции
| ∞ Σ i = 0 |
x[(i-k)Tn]z-i = | ∞ Σ r = -k |
x(rTn) z-(r+k), |
где использована замена переменной i-k = r или i = r+k. С учетом того, что функция x(iTn) рассматривается только при положительном времени iTn, нижний предел суммирования можно заменить нулем и записать
| ∞ Σ r = -k |
x(rTn) z-(r+k) = z-k | ∞ Σ r = 0 |
x(rTn) z-r = z-k x*(z), |
что и доказывает соотношение (1.17).
г) Изображение разности k-ro порядка равно
Z[Δk x(iTn)] = (1-z-1)k x*(z). (1.18)
Докажем это равенство. Используя формулу (1), запишем изображение первой разности
Z[Δ1 x(iTn)] = Z{x(iTn) - x[(i-1)Tn]} = x*(z) - z -1 x*(z) = (1 - z -1)k x*(z).
Из формулы (1.2) для второй разности получаем
Z[Δ2 x(iTn)] = Z{x(iTn) -
2x[(i-1)Tn] + x[(i-2)Tn]} =
= x*(z)- 2z
-1x*(z) + z -2x*(z) = (1-z -1)k
x*(z).
Проделав такую же операцию над третьей разностью (1.3), можно по индукции убедиться в справедливости общего соотношения (1.18).
д) Следующее интересующее нас свойство говорит о том, что изображение x*(z) является рациональной функцией переменной z -1, то есть может быть представлено в виде отношения полиномов
| x*(z) = | a0 + a1z -1 +
a2z -2 + ... + amz -m
β0 + β1z -1 + β2z -2 + ... + βnz -n |
(1.19) |
Убедимся в этом на нескольких конкретных примерах. В простейшем случае дискретная функция состоит из одной дискреты единичной амплитуды, расположенной в момент времени t = kTn (рис. 1.9, а).

Рис. 1.9. Примеры дискретных функций
Такую функцию будем называть единичным дискретным импульсом со следующими свойствами:
| δ [(i-k)Tn] = | { | 1 при i = k |
| 0 при i ≠ k | ||
Найдем изображение этой функции, пользуясь формулой (1.16):
| Z{δ[(i-k)Tn]} = | ∞ Σ i = 0 |
δ[(i-k)Tn] z-i = z-k. |
Если единичный дискретный импульс расположен в начале координат (k = 0), то его изображение
x*(z) = 1.
Теперь положим, что непрерывная огибающая является единичной функцией
x(t) = 1(t).
Тогда соответствующая ей функция х(iТn) называется единичной дискретной функцией (рис. 1.9, б) и равна
| 1 (iTn) = | { | 1 при i = 0, 1, 2, ... ; |
| 0 при i < 0. | ||
Изображение единичной дискретной функции
| Z[1(iTn)] = | ∞ Σ i = 0 |
z-i = 1 + z-1+ z-2 + ... = | 1
1 - z-1 |
где учтено значение суммы бесконечной геометрической прогрессии
| ∞ Σ i = 0 |
qi = 1 + q + q2 + ... = | 1
1 - q |
В заключение найдем изображение дискретной экспоненциальной функции
x(iTn) = e -aiTn
(рис. 1.9, в). Из формулы (1.16) следует, что
| Z[e-aiTn] = | ∞ Σ i = 0 |
e-aiTn z-i = 1 + e-aTn z-1 + e-2aTn z-2 + ... = | 1
1 - e-aTn z-1 |
где также учтена сумма бесконечной геометрической прогрессии. Изображения для некоторых других дискретных функций приводятся в табл. П. 2. Полученные результаты и данные таблицы подтверждают правильность вывода о рациональном характере функции x*(z).
Запись изображения в виде (1.19) позволяет рекуррентным способом вычислять значения оригинала х(iTn) по изображению х*(z). Для этого перепишем выражение (1.19) в другом виде
a0 + a1z -1 + a2z
-2 + ... + amz -m =
(β0 +
β1z -1 + β2z -2 + ... +
βnz -n) [x(0)+ x(1Tn)z -1+
x(2Tn)z -2 + ...]
Приравнивая коэффициенты в левых и правых частях равенства при одинаковых степенях z -k (k = 0, 1, 2,…), получим соотношения для искомой функции x(iTn) при i = 0, 1, 2 ... . Проделаем это для нескольких первых членов:
| a0 = β0 x(0); x(0) = | a0
β0 |
; |
| a1 = β0 x(Tn) + β1 x(0); x(Tn) = | 1
β0 |
[a1 - β1 x(0)]; |
| a2 = β0 x(2Tn) + β1x(Tn) + β2 x(0); x(2Tn) = | 1
β0 |
[a2 - β1 x(Tn) - β2 x(0)]. |
По индукции можно получить следующую формулу для значения процесса в произвольный момент iTn
| x(iTn) = | 1
β0 |
{ai - | i Σ k = 1 |
βk x[(i-k)Tn]}. |
Особенность этого выражения состоит в последовательном (рекуррентном) вычислении переменных, начиная с первого периода следования.
е) Установившееся значение дискретной функции определяется по формуле
| lim i → ∞ |
x(iTn) = | lim z → 1 |
(1- z-1) x*(z). (1.20) |
Изображение дискретной функции можно представить в виде предела
| х*(z) = | lim k → ∞ |
k Σ i = 1 |
x(iTn) z-i, |
а функции с запаздыванием на один период
| z-1 х*(z) = | lim k → ∞ |
k Σ i = 1 |
x[(i-1)Tn] z-i, |
где учитывается равенство x(iTn) = 0 при i < 0.
Тогда при z → 1 можно записать следующее равенство:
| lim z → 1 |
[x*(z)- z-1 x*(z)] = | lim z → 1 |
(1- z-1) x*(z) = | lim k → ∞ |
{x(0) + x(iTn) + |
| + x(2Tn) + ... + x(kTn) - x(0) - x(Tn) - |
| - x(2Tn) - ... - x[(k-1)Tn]} = | lim k → ∞ |
x(kTn), |
которое и доказывает свойство ( 1.20).
Z-преобразование является основным математическим аппаратом ис-следования линейных стационарных дискретных систем и поэтому широко используется в дальнейшем изложении.
Заменяя в формуле (1.10) дискретного преобразования Лапласа переменную р на jω, получаем дискретное преобразование Фурье
| x*(jω) = | k Σ i = 0 |
x(iTn) e-jω Tn i, |
которое определяет частотный спектр дискретного процесса. Чтобы получить спектр из формулы z-преобразования ( 1.16), надо ввести замену переменной
z = ejω Tn
Изучим структуру спектра дискретного процесса, для чего воспользуемся формулой связи (1.13) между изображением х*(р) дискретной функции и ее огибающей. Произведя замену переменной р на jω, находим спектр дискретного процесса в виде
| x*(jω) = | 1
Tn |
∞ Σ k = -∞ |
x[j(ω - kΩ)]. (1.21) |
Таким образом, спектр дискретного процесса является периодической функцией частоты с периодом
| Ω = | 2 π
Tn |
, |
составляющие которой пропорциональны спектру непрерывной огибающей с масштабом 1/Tn. Покажем на графиках характер амплитудно-частотного спектра дискретного процесса |x*(jω)| для следующих двух случаев.
Пусть амплитудный спектр огибающей |x*(jω)| имеет форму, изображенную на верхнем рис. 1.10, а, где ωгр - граничная составляющая спектра, опре-деляющая его ширину. В первом случае положим, что
| ωгр < | Ω
2 |
, |
и тогда в соответствии с формулой (1.21) спектр дискретного процесса примет вид, изображенный на нижнем рис. 1.10, а, и характерный наличием отдельных составляющих, совпадающих по форме с |x*(jω)|. Такая форма спектра называется гребенчатой. Во втором случае положим, что
| ωгр > | Ω
2 |
, |
и тогда спектр примет вид, показанный на рис. 1.10, б, где составляющие спектра перекрываются. По теореме Котельникова, о которой говорилось выше, для восстановления огибающей по дискретным данным о ней требуется выполнение условия
| ωгр < | Ω
2 |
, |
что соответствует спектру на рис. 1.10, а.

Рис. 1.10. Частотный спектр дискретного процесса
Таким образом, частота квантования Ω полезного сигнала должна выбираться так, чтобы спектр дискретного процесса был гребенчатым. Такому же условию должен удовлетворять и спектр выходного процесса у*(jω), что накладывает определенные требования на выбор структуры и параметров дискретной системы. Эти требования рассматриваются ниже.
К динамическим характеристикам дискретных систем, как и в теории непрерывных систем, относят передаточные функции, временные (импульсные, переходные) и частотные характеристики. В литературе принято называть эти характеристики, добавляя слово "дискретная" (например, "дискретная передаточная функция" - ДПФ, "дискретная переходная характеристика" - ДПХ и т. д.). Здесь мы ограничимся написанием символа * и аргумента iTn, подчеркивающих принадлежность характеристик дискретным системам. Перейдем к их рассмотрению, для чего запишем конечно-разностное уравнение системы
| ^ C0 |
yn(iTn) + | ^ C1 |
Δ1 y(iTn) + ... + | ^ Cn |
Δn y(iTn) = |
| = | ^ b0 |
x(iTn) + | ^ b1 |
Δ1 x(iTn) + ... + | ^ bm |
Δm x(iTn). |
Возьмем z-преобразование от обеих его частей с учетом правила нахождения изображения конечной разности. В итоге получим операторное уравнение
| ^ C0 |
y*(z) + | ^ C1 |
(1 - z-1) y*(z) + ... + | ^ Cn |
(1 - z-1)n y*(z) = |
| ^ b0 |
x*(z) + | ^ b1 |
(1 - z-1) x*(z) + ... + | ^ bm |
(1 - z-1)m x*(z), |
из которого находим передаточную функцию дискретной системы в виде отношения изображений
| K^yx(z) = | y*(z) | = | ^ b0 |
+ | ^ b1 |
(1 - z-1) + ... + | ^ bm |
(1 - z-1)m | = | P*(z) | . (1.22) |
|
|
|
| |||||||||
| x*(z) | ^ c0 |
+ | ^ c1 |
(1 - z-1) + ... + | ^ cn |
(1 - z-1)n | D*(z) | ||||
По своей структуре эта функция совпадает с передаточной функцией непрерывной системы, если вместо оператора р подставить оператор (1-z-1). Когда разностное уравнение задано в рекуррентной форме
c0 y(iTn) + c1 y[(i-1)Tn]
+ ... + cn y[(i-n)Tn] =
= b0
x(iTn) + b1 x[(i-1)Tn] + ... + bm
x[(i-m)Tn],
ему будет соответствовать операторное уравнение
c0 y*(z) + c1 z-1 y*(z) + ... +
cn z-n y*(z) =
= b0 x*(z) + b1
z-1 x*(z) + ... + bm z-m x*(z).
После преобразований получим вторую форму записи передаточной функции
| K^yx(z) = | y*(z)
x*(z) |
= | b0 + b1 z-1 + ... +
bm z-m
c0 + c1 z-1 + ... + cn z-n |
= | P*(z)
D*(z) |
. (1.23) |
Формулы (1.22) и (1.23) эквивалентны и могут быть получены друг из друга. С их помощью изображение выходного процесса по изображению входного процесса находится как произведение
y*(z) = x*(z)K*yx(z). (1.24)

Рис. 1.11. Соединение дискретных звеньев
Благодаря одинаковой структуре передаточной функции дискретной системы и передаточной функции непрерывной системы остаются справедливыми все правила структурных преобразований, применяемые для непрерывных систем. Так, для последовательного соединения дискретных звеньев (рис. 1.11,а)
K*yx(z) = K*1(z) K*2(z)
Для параллельного соединения (рис. 1.11,б)
K*yx(z) = K*1(z) ± K*2(z)
Для соединения с обратной связью (рис. 1.11, в)
| K*yx(z) = | K*1(z)
1 ± K*1(z) K*2(z) |

Рис. 1.12. Импульсная характеристика дискретной системы
При нахождении временных характеристик в качестве типовых воздействий используются единичный дискретный импульс и единичная дискретная функция. Импульсной характеристикой линейной дискретной системы Kyx(iTn) (рис. 1.12, а) называется реакция на единичный дискретный импульс δ(iTn) при нулевых начальных условиях. С ее помощью можно определить реакцию системы на произвольное воздействие х(iTn). Рассматривая рис. 1.12,б, нетрудно понять, что значение выходного процесса y(iTn) можно подсчитать по формуле
| y(iTn) = | ∞ Σ k = 0 |
x(kTn) kyx [(i-k)Tn]. |
Если учесть условие физической реализуемости импульсной характеристики
kyx[(i-k)Tn] = 0
при i < k, то эту формулу можно переписать, заменив верхний предел суммы бесконечностью, то есть
| y(iTn) = | ∞ Σ k = 0 |
x(kTn) kyx [(i-k)Tn]; (1.25) |
kyx[(i-k)Tn] = 0 при i < k.
Это соотношение называется формулой свертки, оно аналогично интегралу свертки в теории непрерывных систем. Возьмем z - преобразование от формулы свертки (1.19) и найдем изображение выходного процесса через импульсную характеристику
| y*(z) = | ∞ Σ i = 0 |
∞ Σ k = 0 |
x(kTn) kyx [(i-k)Tn] z-i (zk z-k). |
Мы искусственно домножили слагаемые на единичный множитель в форме
1 = zk z-k.
Поменяем местами порядок суммирования, произведем перегруппировку сомножителей и заменим переменную i-k = r, i = k+r, после чего будем иметь
| y*(z) = | ∞ Σ k = 0 |
x(kTn) z-k | ∞ Σ i = 0 |
kyx [(i-k)Tn] z-(i-k) = | ∞ Σ k = 0 |
x(kTn) z-k | ∞ Σ i = 0 |
kyx (rTn) z-r. |
По условию физической реализуемости kyx(rTn) = 0 при r < 0, поэтому нижний предел у внутренней суммы можно заменить нулем и она не будет зависеть от переменной k, в результате чего суммы станут независимыми и их можно поменять местами. Заметим, что первая сумма
| ∞ Σ k = 0 |
x(kTn) z-k = x*(z), |
поэтому изображение выходной переменной станет равным
| y*(z) = x*(z) | ∞ Σ r = 0 |
kyx (rTn) z-r. |
Сравнивая это равенство с формулой (1.24), получаем выражение для передаточной функции через импульсную характеристику в виде
| K*yx(z) = | ∞ Σ i = 0 |
kyx (iTn) z-i. (1.26) |
Таким образом, передаточная функция дискретной системы является z-преобразованием от импульсной характеристики.
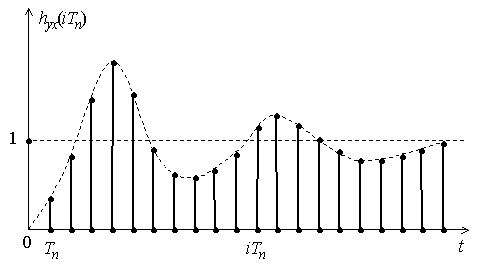
Рис. 1.13. Переходная характеристика дискретной системы
Переходной характеристикой линейной дискретной системы hyx(iTn) называется реакция на единичную дискретную функцию 1(iTn) при нулевых начальных условиях (рис. 1.13). Подставляя в формулу свертки (1.25) функцию
x(iTn) = 1(iTn),
найдем связь между переходной и импульсной характеристиками в виде
| hyx(iTn) = | i Σ k = 0 |
1(kTn) kyx [(i-k)Tn] = | i Σ k = 0 |
kyx [(i-k)Tn] = |
| = | i Σ r = -k |
kyx (rTn) = | i Σ r = 0 |
kyx (rTn). ( 1.26) |
Переходная характеристика находится в виде суммы значений импульсной характеристики. Так как изображение единичного воздействия согласно табл. П. 2 равно
| Z[1(iTn)] = | 1
1 - z-1 |
, |
то изображение переходной характеристики
| Z[hyx(iTn)] = | 1
1 - z-1 |
K*yx(z). |
Перейдем к рассмотрению частотных характеристик, для чего в передаточной функции K*yx(z) заменим переменную
z = е j ω Tn
и обозначим полученную функцию через K*yx(z). Форму частотной характеристики дискретной системы удобнее всего получить, если вначале рассмотреть непрерывную огибающую kyx(t) импульсной характеристики kyx(iTn). На рисунке 1.12, а эта огибающая показана пунктиром. Возьмем преобразование Лапласа от этой непрерывной функции и назовем ее передаточной функцией системы по огибающей
| Кyx(p) = | ∞ ∫ 0 |
kyx(t) e-ptdt. |
Тогда в соответствии с формулой связи (1.13) между изображениями дискретной и непрерывной функций можно записать, что
| Кyx(p) = | 1
Tn |
∞ Σ k = -∞ |
Кyx(p)(p - jkΩ). |
Заменяя в этом равенстве p на jω, получаем формулу связи между частотными характеристиками дискретной системы и частотной характеристикой по огибающей
| Кyx(jω) = | 1
Tn |
∞ Σ k = -∞ |
Кyx[j(ω - kΩ)]. (1.27) |
По своему содержанию это выражение аналогично спектру дискретного процесса
(1.21). Рассмотрим амплитудно-частотную характеристику дискретной системы
|K*yx(jω)| в соответствии с амплитудно-частотной
характеристикой по огибающей |K*yx(jω)|. Пусть форма
|Kyx(jω)| имеет вид, показанный на рис. 1.14, а, где ω0 -
полоса пропускания такая, что при ω > ω0 |Kyx(jω)| → 0.
Частотная характеристика дискретной системы при ω0 <  показана на рис.
1.14, а, а при ω0 >
показана на рис.
1.14, а, а при ω0 >  - на рис. 1.14, б.
- на рис. 1.14, б.

Рис. 1.14. Амплитудно-частотные характеристики инерционных дискретных звеньев
Дискретные системы, у которых ω0 <  , обладают свойством гребенчатых
фильтров. Как будет показано ниже, эти свойства оказываются необходимыми для
качественной работы дискретных следящих систем.
, обладают свойством гребенчатых
фильтров. Как будет показано ниже, эти свойства оказываются необходимыми для
качественной работы дискретных следящих систем.
Сложную передаточную функцию дискретной системы удобно представлять в виде произведения передаточных функций типовых звеньев не выше второго порядка, как это делалось для непрерывных систем. Так как передаточная функция К*(z), записанная формулой (1.23), по своей структуре аналогична передаточной функции непрерывной системы
| Kyx(p) = | y(p)
x(p) |
= | b0 + b1 p + ... + bm
pm
c0 + c1 p + ... + cn pn |
= | P(p)
D(p) |
, |
где роль р играет разностный оператор (1-z-1), то выражения типовых дискретных звеньев остаются похожими на соответствующие выражения непрерывных. Классификация типовых дискретных звеньев и некоторые их характеристики даются в табл. П. 4. Аналогия между дискретными и непрерывными звеньями имеет не только внешний, но и существенный характер. Особенно наглядно это видно на примере частотных характеристик, которые для дискретных звеньев получаются заменой
z = e jωTn
в передаточной функции К*(z). Особенность этих выражений состоит в том, что параметр τ в них является безразмерной величиной, поскольку оператор
(1 - z-1)
также не имеет размерности. Называть поэтому параметр τ постоянной времени можно лишь условно. Несмотря на указанное отличие, между типовыми дискретными и непрерывными звеньями существует глубокая аналогия, которая наглядно видна при сравнении частотных характеристик. Напомним, что для получения частотной характеристики дискретной системы надо в передаточной функции К*(z) заменить
z = e jωTn
или вместо разностного оператора (1 - z-1) взять
(1 - e -jωTn).
Если ωTn << 1, что соответствует низким частотам ω << Ω, то оператор
1 - e -jωTn → jωTn,
а это приводит к практически полному совпадению с частотными характеристиками типовых непрерывных звеньев с постоянной времени
T = τ Tn,
Таким образом, в области ω, близких к нулю, частотные характеристики дискретных совпадают с характеристиками соответствующих непрерывных звеньев. Так, например, при ω = 0 частотная характеристика суммирующего (дискретного интегрирующего) звена равна
K*(jω) = ∞,
а апериодического и колебательного звеньев - единице. С ростом частоты ω от 0
до  амплитудно-частотные характеристики этих звеньев уменьшаются. В дальнейшем они
меняются периодически вдоль оси ω с периодом
амплитудно-частотные характеристики этих звеньев уменьшаются. В дальнейшем они
меняются периодически вдоль оси ω с периодом  . На рисунке 1.14 показаны АЧХ:
а-суммирующего, б-апериодического, в-колебательного звена при различных
значениях параметра ξ. Идеальное разностное (дискретное дифференцирующее) звено
при ω = 0 имеет
. На рисунке 1.14 показаны АЧХ:
а-суммирующего, б-апериодического, в-колебательного звена при различных
значениях параметра ξ. Идеальное разностное (дискретное дифференцирующее) звено
при ω = 0 имеет
K*(jω) = 0,
а разностные первого и второго порядка -1. То же самое имеет место и у
соответствующих непрерывных звеньев. С ростом частоты ω от 0 до  АЧХ разностных
звеньев возрастает, что и показано на рис. 1.15 для идеального разностного звена
(а), разностного звена первого порядка (б) и разностного звена второго порядка
(в). Зная характер поведения частотных характеристик типовых дискретных звеньев,
можно судить о желаемой структуре дискретной следящей системы и, следовательно,
о ее желаемой передаточной функции.
АЧХ разностных
звеньев возрастает, что и показано на рис. 1.15 для идеального разностного звена
(а), разностного звена первого порядка (б) и разностного звена второго порядка
(в). Зная характер поведения частотных характеристик типовых дискретных звеньев,
можно судить о желаемой структуре дискретной следящей системы и, следовательно,
о ее желаемой передаточной функции.

Рис. 1.15. Амплитудно-частотные характеристики разностных дискретных звеньев
Дискретная следящая система (рис. 1.16) предназначена для воспроизведения задающего воздействия х(iТn), и в идеальном случае выходной процесс в ней должен равняться входному, то есть
y(iTn) = x(iTn).
Выполнению этого равенства препятствуют два фактора: наличие возмущающих воздействий и инерционность системы. Оба эти фактора существенно влияют на выбор формы частотной характеристики замкнутой системы.

Рис. 1.16. Линейная дискретная следящая система
Частотный спектр задающего воздействия х*(jω) расположен в области низких частот и имеет граничную частоту ωгр ( рис. 1.17). В соответствии с теоремой Котельникова, частота квантования сигнала должна удовлетворять условию Ω > ωгр.

Рис. 1.17. Амплитудно-частотная характеристика дискретной следящей системы
Для достаточно полного воспроизведения спектра задающего воздействия на фоне
широкополосных помех частотная характеристика замкнутой следящей системы
K*yx(jω) должна быть близка к 1 в диапазоне 0 ≤ ω ≤
ωгр и к нулю - в диапазоне ωгр < ω ≤  . Этому условию, в частности,
удовлетворяет кривая амплитудно-частотной характеристики
|K*yx(jω)| на рис. 1.17. Стремлению
K*yx(jω) → 0 при ω →
. Этому условию, в частности,
удовлетворяет кривая амплитудно-частотной характеристики
|K*yx(jω)| на рис. 1.17. Стремлению
K*yx(jω) → 0 при ω →  соответствуют и условия
естественной инерционности элементов САУ. В итоге, если рассматривать всю
область частот, АЧХ замкнутой дискретной следящей системы должна иметь вид,
показанный на рис. 1.18, то есть соответствовать характеристике гребенчатого
фильтра.
соответствуют и условия
естественной инерционности элементов САУ. В итоге, если рассматривать всю
область частот, АЧХ замкнутой дискретной следящей системы должна иметь вид,
показанный на рис. 1.18, то есть соответствовать характеристике гребенчатого
фильтра.
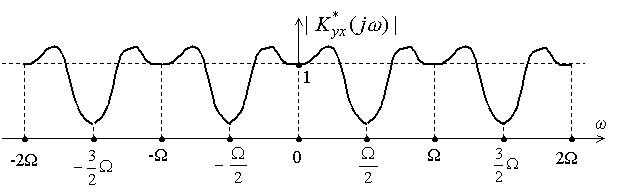
Рис. 1.18. Амплитудно-частотная характеристика гребенчатого фильтра
Чтобы получить заданную K*yx(jω), надо сформировать вполне определенную частотную характеристику разомкнутой системы (рис. 1.16) K*(jω). Очевидно, что требования к последней аналогичны тем требованиям, которые предъявляются к частотным характеристикам разомкнутых непрерывных следящих систем. Так, чтобы обеспечить равенство
K*yx(jω) ≈ 1
на частотах ω = 0 и ω, кратных Ω (см. рис. 1.18), необходимо иметь
K*(jω) → 0, что достигается включением в состав системы суммирующих
(дискретных интегрирующих) звеньев или усилительных звеньев с очень большим
коэффициентом усиления. Чтобы обеспечить условие K*yx(jω)
→ 0 при ω →  в
состав разомкнутой системы надо включать инерционные (апериодические или
колебательные) звенья. Согласование хода частотных характеристик в указанных
областях может быть обеспечено разностными (дискретными дифференцирующими)
звеньями.
в
состав разомкнутой системы надо включать инерционные (апериодические или
колебательные) звенья. Согласование хода частотных характеристик в указанных
областях может быть обеспечено разностными (дискретными дифференцирующими)
звеньями.
Анализ частотных характеристик показывает, что структура дискретной следящей системы, определяемая звеньями, входящими в состав разомкнутой системы, аналогична структуре непрерывных следящих систем и соответственно аналогичны и передаточные функции сравниваемых систем. Передаточная функция дискретной разомкнутой следящей системы (рис. 1.16), например, может быть получена из разностного уравнения, записанного в конечно-разностной форме
| ^ a0 |
y(iTn) + | ^ a1 |
Δ1 y(iTn) + ... + | ^ an |
Δn y(iTn) = |
| = | ^ b0 |
r(iTn) + | ^ b1 |
Δ1 r(iTn) + ... + | ^ bm |
Δm r(iTn), | (1.28) |
в виде
| K*(z) = | = | ^ b0 |
+ | ^ b1 |
(1 - z-1) + ... + | ^ bm |
(1 - z-1)m | = | P*(z) | . (1.29) |
|
|
| |||||||||
| ^ a0 |
+ | ^ a1 |
(1 - z-1) + ... + | ^ an |
(1 - z-1)n | Q*(z) | ||||
В выражениях (1.28) и (1.29) коэффициенты  и
и  определяются параметрами
дискретной системы. Порядок астатизма ν определяется количеством коэффициентов
определяются параметрами
дискретной системы. Порядок астатизма ν определяется количеством коэффициентов
 0 =
0 =  1 = ... =
1 = ... =
 ν -
1 = 0 или, что одно и то же, количеством суммирующих звеньев.
ν -
1 = 0 или, что одно и то же, количеством суммирующих звеньев.
Уравнение замкнутой следящей системы получается из выражения (1.28) путем замены r(iTn) = x(iTn) - y(iTn) и после группировки слагаемых принимает вид
| ^ c0 |
y(iTn) + | ^ c1 |
Δ1 y(iTn) + ... + | ^ cn |
Δn y(iTn) = |
| = | ^ b0 |
y(iTn) + | ^ b1 |
Δ1 y(iTn) + ... + | ^ bm |
Δm y(iTn), | (1.30) |
где коэффициенты
 =
=  +
+  .
.
Передаточная функция замкнутой системы, получаемая из формулы (1.30) или по рис. 1.16, оказывается равной
| K*yx(z) = | K*(z) | = | ^ b0 |
+ | ^ b1 |
(1 - z-1) + ... + | ^ bm |
(1 - z-1)m | = | P*(z) | . (1.31) |
|
|
|
| |||||||||
| 1 + K*(z) | ^ c0 |
+ | ^ c1 |
(1 - z-1) + ... + | ^ cn |
(1 - z-1)n | D*(z) | ||||
где полином знаменателя
D*(z) = P*(z) + Q*(z).
В следящих системах ошибка e(iTn) совпадает с рассогласованием r(iTn) и, следовательно, передаточная функция ошибки по задающему воздействию согласно рис. 1.16 равна
| K*ex(z) = 1 - K*yx(z) = | 1 | = | ^ a0 |
+ | ^ a1 |
(1 - z-1) + ... + | ^ an |
(1 - z-1)n | = | Q*(z) | . (1.32) |
|
|
|
| |||||||||
| 1 + K*(z) | ^ c0 |
+ | ^ c1 |
(1 - z-1) + ... + | ^ cn |
(1 - z-1)n | D*(z) | ||||
Передаточная функция ошибки по возмущающему воздействию, как и в непрерывных системах, равна
K*ev(z) = - K*yv(z),
то есть с точностью до знака совпадает с передаточной функцией системы по этому воздействию и согласно рис. 1.16 равна
| K*ev(z) = - K*yv(z) = | K*v(z)
1 + K*(z) |
, (1.33) |
где K*v(z) - передаточная функция по возмущающему воздействию разомкнутой системы.
Таким образом, соотношения (1.28) - (1.33) для дискретных следящих систем имеют ту же структуру, что и соответствующие им соотношения для непрерывных следящих систем.
Отметим, что если исходное уравнение разомкнутой следящей системы (1.28) записывается в рекуррентной форме (см. п. 1.3)
a0 y(iTn) + a1 y[(i-1)Tn]
+ ... + an y[(i-n)Tn] =
= b0
r(iTn) + b1 r[(i-1)Tn] + ... + bm
r[(i-m)Tn],
то уравнение замкнутой примет вид
c0 y(iTn) + c1 y[(i-1)Tn]
+ ... + cn y[(i-n)Tn] =
= b0
x(iTn) + b1 x[(i-1)Tn] + ... + bm
x[(i-m)Tn]. (1.34)
При этом полиномы P*(z), Q*(z) и D*(z) меняют свою структуру и передаточные функции дискретной следящей системы записываются в следующем виде:
| K(z) = | b0 + b1 z-1 + ... +
bm z-m
a0 + a1 z-1 + ... + an z-n |
= | P*(z)
Q*(z) |
. (1.35) |
| K^yx(z) = | b0 + b1 z-1 + ... +
bm z-m
c0 + c1 z-1 + ... + cn z-n |
= | P*(z)
D*(z) |
. (1.36) |
| K^ex(z) = | a0 + a1 z-1 + ... +
an z-n
c0 + c1 z-1 + ... + cn z-n |
= | Q*(z)
D*(z) |
. (1.37) |
Использование передаточных функций следящих систем в виде соотношений (1.29), (1.31) и (1.32) или соотношений (1.35) - (1.37) определяется характером решаемой задачи.
Использование цифровых методов обработки информации в системах автоматического управления позволяет реализовывать сложные алгоритмы управления и обеспечивать их быструю сменяемость. Кроме того, цифровые устройства, как правило, более надежны в работе и имеют меньшие габариты и массу. Автоматические системы, полностью построенные на цифровых элементах, называются цифровыми САУ (ЦСАУ). Особенно широкое распространение ЦСАУ получили в радиотехнических системах для обработки информации о параметрах радиосигналов. Например, в радиолокационных системах эти параметры (амплитуда, частота, фаза и др.) несут информацию о координатах объектов, поэтому в них используют ЦСАУ для слежения за угловыми координатами, дальностью и скоростью перемещения целей. В радиотехнических следящих системах входная информация передается с помощью радиосигналов, а выходная, как правило, в виде электрических сигналов, что дает возможность выполнить систему только из электронных элементов и устройств. В том случае, когда выходная информация должна выдаваться в виде линейных или угловых перемещений, используют электрические и электромеханические цифровые элементы. Сигналы в ЦСАУ формируются в виде последовательности импульсов, образующих некоторый код, с помощью которого записываются мгновенные значения процессов, подлежащих обработке.
Кодовая модуляция сигналов приводит к тому, что информация в системе квантуется как по времени, так и по уровню. Квантование по времени происходит из-за импульсного "характера сигналов, в результате чего полезная информация выдается в виде дискретной функции x(iTn). Квантование по уровню происходит за счет конечного числа импульсов в коде, называемого числом разрядов. При конечном числе разрядов можно отобразить лишь конечное число дискретных значений передаваемого процесса. Например, в случае двоичного кода при числе разрядов q максимальное число дискретных значений процесса
N = 2q - 1.
Так, если код имеет 8 разрядов, то N = 225; если q = 12, то N = 4095. При заданном числе разрядов передаваемый процесс x(iTn) может отображаться не более чем N дискретными значениями.

Рис. 1.19. Два способа квантования по уровню
Если максимальное значение процесса равно xmах, а минимальное xmin, то шаг квантования по уровню
| Δ = | xmах - xmin
N |
. |
В результате квантования по уровню получается процесс  (iTn), который будет
лишь приближенно отражать характер изменения процесса x(iTn). Ошибка
приближения (округления) будет зависеть от шага квантования и способа
квантования по уровню, два из которых показаны на рис. 1.19. В первом случае
квантование по уровню происходит по правилу: принимается значение
(iTn), который будет
лишь приближенно отражать характер изменения процесса x(iTn). Ошибка
приближения (округления) будет зависеть от шага квантования и способа
квантования по уровню, два из которых показаны на рис. 1.19. В первом случае
квантование по уровню происходит по правилу: принимается значение  (iTn), ближайшее к
x(iTn) (рис. 1.19, а). Во втором принимается значение
(iTn), ближайшее к
x(iTn) (рис. 1.19, а). Во втором принимается значение  (iTn), ближайшее к
x(iTn) снизу для x(iTn) > 0 и сверху для
x(iTn) < 0 (рис. 1.19,б). Квантование по уровню является
безынерционным нелинейным преобразованием типа многоступенчатой релейной
характеристики, показанной на рис. 1.19, и обозначается в виде функции
(iTn), ближайшее к
x(iTn) снизу для x(iTn) > 0 и сверху для
x(iTn) < 0 (рис. 1.19,б). Квантование по уровню является
безынерционным нелинейным преобразованием типа многоступенчатой релейной
характеристики, показанной на рис. 1.19, и обозначается в виде функции

Статическая характеристика квантователя для первого способа квантования показана на рис. 1.20, а, а для второго - на рис. 1.20, б. Прямые, проходящие через начало координат, соответствуют случаю линейного преобразования. Из характеристик на рис. 1.20 видно, что ошибка округления при первом способе квантования равна 0.5Δ, а при втором - Δ. Хотя первый способ квантования обладает более высокой точностью, однако его техническая реализация сложнее второго. Ошибка округления является инструментальной погрешностью ЦСАУ, определяющей точность работы в статике, и большей точности в цифровых системах достигнуть невозможно. Величину ошибок округления можно уменьшить путем увеличения числа разрядов кода, однако это приводит к усложнению конструкции цифровых элементов. В динамических условиях работы ошибки могут быть значительно выше ошибок округления и играют определяющую роль, поэтому методике их расчета в дальнейшем уделяется особое внимание. Наличие квантования по уровню может приводить к появлению автоколебаний, амплитуда и частота которых зависят от шага квантования Δ.

Рис. 1.20. Статические характеристики квантователей
Таким образом, цифровая обработка информации имеет ряд специфических особенностей, которые надо учитывать в процессе исследования ЦСАУ.

| Рис. 1.21. Структурная схема квантователя | Рис. 1.22. Функциональная схема ЦСАУ |

Рис. 1. 23. Функциональная схема ЦВМ
Цифровое представление информации в ЦСАУ можно отобразить с помощью двух последовательно выполняемых операций: квантования по времени и квантования по уровню. Квантование по времени является операцией линейной, а по уровню - нелинейной, в результате чего ЦСАУ относятся к классу нелинейных систем. На структурных схемах операцию квантования по уровню отображают нелинейным звеном с характеристикой (рис. 1.21). Наиболее широкое распространение получили электронные цифровые следящие системы на базе цифровых вычислительных машин (ЦВМ), функциональная схема которых изображена на рис. 1.22. В цифровом измерителе рассогласования (ЦИР) формируется в цифровой форме рассогласование
 ,
,
которое поступает и обрабатывается на ЦВМ. На рисунке 1.23 изображена упрощенная функциональная схема машины, где ВВ и ВЫВ - устройства ввода и вывода; ПР - процессор; ОП - оперативная память; ВП - внешняя память. ПР предназначен для проведения операций над числами, ОП - для хранения промежуточных результатов и команд, ВП - для хранения алгоритмов обработки информации и исходных данных. Главной особенностью ЦВМ является работа в реальном масштабе времени. Это значит, что вся обработка поступающей информации должна заканчиваться за время ТП (период квантования процессов по времени), и это накладывает жесткие требования на быстродействие машины, а оно, в свою очередь, часто определяет минимальное значение Тn. Так как частота квантования
| Ω = | 2 π
Tn |
должна удовлетворять теореме Котельникова (п.1.2), то быстродействие ЦВМ может существенно влиять на качество работы системы. Время обработки информации машиной Т0 складывается из времени ввода и вывода данных, времени обращения к памяти и времени проведения операций в процессоре. При работе в реальном масштабе времени
T0 = α Tn,
где коэффициент 0 < α ≤ 1. Таким образом, выдача данных из ЦВМ будет происходить с запаздыванием на время αTn относительно момента их поступления, поэтому машина в составе ЦСАУ может рассматриваться как запаздывающее звено с передаточной функцией
Kцвм(p) = e-p α Tn.
Так как в теории z-преобразования e-p Tn = z-1, то передаточная функция ЦВМ как дискретного звена равна K*цвм(p) = z-α где 0 ≤ α ≤ 1.
За время T0 = α Tn информация обрабатывается в соответствии с заложенными в машину алгоритмами, которые задаются в виде разностных уравнений. Если эти уравнения линейные, например вида (1.5) или (1.8), то алгоритму будет соответствовать передаточная функция K*α(z), которая в виде дискретного звена должна отображаться на структурной схеме.

Рис. 1. 24. Структурная схема цифровой следящей системы
Подводя итоги всему сказанному выше, можно представить структурную схему ЦСАУ в виде рис. 1.24, где суммирующими и нелинейными звеньями обозначен цифровой измеритель рассогласования, запаздывающим звеном z-α - цифровая вычислительная машина, а дискретным звеном K*α(z) - линейный алгоритм обработки информации. Последовательное соединение запаздывающего и алгоритмического звеньев образует передаточную функцию линейной части ЦСАУ
K*(z) = z-α K*α(z).
В том случае, когда период квантования Tn определяется только быстродействием ЦВМ, можно полагать α = 1, а если время обработки T0 << Tn, то α = 0. Выбором достаточно большого числа разрядов цифрового кода можно сделать шаг квантования Δ и ошибку округления настолько малыми, что влиянием нелинейного звена можно пренебречь и считать ЦСАУ линейной дискретной системой.
Исследование дискретных систем начинается с оценки их принципиальной работоспособности, то есть устойчивости. В классе линейных систем задача решается так же, как и в теории линейных непрерывных САУ, но с учетом особенностей, связанных с квантованием сигналов, и вытекающей из них специфики аппарата.
Напомним, что устойчивость непрерывных линейных систем определялась по поведению переходной составляющей yn(t) общего решения однородного дифференциального уравнения исследуемой системы. Аналогично решается задача и для дискретных систем, описываемых линейными разностными уравнениями (1.34). Общее решение таких уравнений представляет собой сумму
y(iTn) = yв(iTn) + yn(iTn)
где yв(iTn) - вынужденная составляющая процесса, зависящая от внешнего воздействия, а
| yn(iTn) = | n Σ k = 1 |
Ak zik, (2.1) |
- переходная составляющая, представляющая собой сумму экспоненциальных дискретных функций
zik = ekpiTn
с начальными значениями Ak. В выражении (2.1) zk - корни характеристического уравнения замкнутой системы D*(z) = 0 (или уравнения Q*(z) = 0, если исследуется устойчивость разомкнутой системы), зависящие от параметров системы.
Дискретная система называется устойчивой, если с течением времени yn(iTn) стремится к нулю. Примеры поведения переходной составляющей показаны на рис. 2.1, где позициями а и б обозначены монотонные, а в и г - колебательные процессы устойчивых и неустойчивых систем. При i → ∞ yn(iTn) будет равна нулю, если все корни zk характеристического уравнения D*(z) = 0 по модулю будут меньше единицы: |zk| < 1.

Рис. 2.1. Устойчивые (а и в) и неустойчивые (б и г) процессы в дискретных системах
Таким образом, необходимое и достаточное условие устойчивости линейных дискретных систем может быть сформулировано так: замкнутая система будет устойчивой, если корни характеристического уравнения D*(z) = 0 находятся внутри круга единичного радиуса. Условия устойчивости на комплексной плоскости иллюстрируются рис. 2.2. Если речь идет об устойчивости разомкнутой системы, то оценивается расположение корней уравнения Q*(z) = 0 и применяются сформулированные выше условия. Исследование дискретных систем автоматического управления базируется в основном на аппарате z-преобразования. Определение при этом устойчивости по расположению корней характеристического уравнения относительно круга единичного радиуса в реальных случаях может быть сложным и неудобным (высокий порядок уравнения, повторение громоздкой процедуры вычисления при неудовлетворительных предыдущих результатах и т.п.). Для упрощения задачи, как и в случае непрерывных линейных систем, можно использовать критерии устойчивости, позволяющие избежать решения характеристического уравнения D*(z) = 0.
Естественно попытаться при этом приспособить уже известные критерии теории непрерывных систем, связывающие устойчивость с расположением корней характеристического уравнения в левой полуплоскости, к анализу дискретных систем, устойчивых в случае расположения корней своего характеристического уравнения внутри круга единичного радиуса. Очевидно, что задача сводится к преобразованию единичного круга в полуплоскость, которое может быть произведено подстановкой
| z = | 1 + w
1 - w |
или w = | z - 1
z + 1 |
, (2.2) |
называемой билинейным или w-преобразованием. Если комплексное число w представить в алгебраической форме
w = β + jν,
то условие устойчивости дискретной системы |zk| < 1 примет вид
 (2.3)
(2.3)
Неравенство (2.3) соблюдается только тогда, когда βk < 0. Следовательно, если ввести подстановку (2.2) в характеристический полином D*(z), то можно получить характеристическое уравнение в форме
D*(w) = 0.
Если корни этого уравнения лежат в левой полуплоскости комплексной плоскости w, то дискретная система устойчива. Отображение единичного круга в полуплоскость показано на рис. 2.3, где заштрихованы области расположения корней характеристических уравнений устойчивой системы.

| Рис. 2.2. Условия устойчивости в плоскости корней (а) | Рис. 2.3. Преобразование единичного круга в полуплоскость (б) |
Отметим, что переменная w является аналогом переменной р в теории непрерывных систем, но в отличие от последней безразмерна. Если анализ системы ведется в частотной области, то по аналогии с заменой р = jω в непрерывных системах вводят подстановку w = jν в дискретных системах. Связь безразмерной псевдочастоты ν с размерной w определяется из условия (2.2) подстановками

откуда псевдочастота
| ν = tg | ω Tn
2 |
. (2.4) |
Введение билинейного преобразования (2.2) позволяет использовать для анализа устойчивости дискретных систем алгебраические и частотные критерии устойчивости непрерывных систем. Методика решения задачи рассматривается на примере.
Пример 2.1.
Передаточная функция разомкнутой следящей системы (рис. 1.15) задана в виде
| K*(z) = | k z-1
1 - z-1 |
= | P*(z)
Q*(z) |
, |
то есть система состоит из запаздывающего и суммирующего звеньев. Определим условия устойчивости замкнутой дискретной системы, используя способы, описанные выше.
1. Непосредственное решение разностного уравнения.
Для замкнутой системы получаем
| K*yx(z) = | k z-1
1 - (1 - k)z-1 |
= | P*(z)
D*(z) |
= | y*(z)
x*(z) |
. (2.5) |
Разностное уравнение в z-изображениях
y*(z) - (1 - k)z-1y*(z) = k z-1x*(z). (2.6)
Однородное разностное уравнение в оригиналах, определяющее переходную составляющую:
yn(iTn) - (1 -
k)yn[(i-1)Tn] = 0 или
yn(iTn) =
(1 - k)yn[(i-1)Tn].
Решение этого уравнения при
yn(-iTn) = 0 и yn(0) = A1
записывается в виде
yn(iTn) = (1 - k)A1; (1 -
k)2A1; ... ;
yn(iTn) = (1 -
k)iA1;
и для различных значений коэффициента k приведено на рис. 2.4. Если k = 0 или k = 2, то переходная составляющая не затухает. При k = 0.5 процесс имеет затухающий апериодический, а при k = 1.5 - затухающий колебательный характер. Если k = 1, то переходный процесс в системе практически отсутствует (заканчивается к первому периоду). Таким образом, условие устойчивости
| lim i = 0 |
yn(iTn) = 0 |
соблюдается в исследуемой системе при 0 < k < 2. (2.7)

Рис. 2.4. Переходные процессы в дискретной системе при различных коэффициентах преобразования
2. Суждение об устойчивости по корням характеристических уравнений.
Характеристическое уравнение в z - изображениях имеет согласно выражению (2.5) вид
D*(z) = 1 - (1 - k) z-1 = 0. (2.8)
Корень этого уравнения z1 = 1 - k по условиям устойчивости должен находиться внутри круга единичного радиуса, то есть |z1| = |1 - k| < 1 и мы вновь приходим к неравенству (2.7).
3. Использование алгебраического критерия Гурвица.
Вводя подстановку
| z = | 1 + w
1 - w |
в формулу (2.8), получим характеристическое уравнение замкнутой системы в виде
| D*(z) = 1 - (1 - k) | 1 - w
1 + w |
= k + (2 - k)w = 0. |
По критерию Гурвица система первого порядка устойчива, если все коэффициенты характеристического уравнения положительны, то есть k > 0 и 2 - k > 0. Отсюда для устойчивой системы 0 < k < 2.
4. Использование логарифмического критерия.
Вводя подстановку
| z = | 1 + w
1 - w |
получим выражение для исходной передаточной функции разомкнутой системы
| K*(w) = |
|
= | k(1 - w)
2w |
. (2.9) |
Если по аналогии с непрерывными системами, где вводится замена p = jω, подставить в выражение (2.9) w = jν, то можно построить частотные характеристики разомкнутой дискретной системы и по ним судить об устойчивости замкнутой системы. Для использования логарифмического критерия на рис. 2.5 построены ЛЧХ, соответствующие выражению (2.9).

Рис. 2.5. Логарифмические характеристики дискретной системы при различных коэффициентах преобразования
При построении учтено, что k / 2ω - аналог передаточной функции соединения усилительного и интегрирующего звеньев, а (1 - w) - аналог передаточной функции дифференцирующего звена 1-го порядка неминимально-фазового типа. У этого звена
L(ν) = 20 lg|1 - w| = 20 lg  и ψ(ν) = - arctg(ν);
и ψ(ν) = - arctg(ν);
На рис. 2.5 показаны ЛАХ системы для k < 2, k = 2 и k > 2. Согласно, логарифмическому критерию замкнутая система будет устойчивой только при k / 2 < 1, так как в любом другом случае частота среза равна бесконечности и при этом φ(νc) = - 180° (см. рис. 2.5). Отметим, что рассматриваемая система теряет устойчивость на половинной частоте квантования. Действительно, согласно формуле (2.4)
| ν = tg | ωTn
2 |
и при ν = ∞ | ωTn
2 |
= | π
2 |
Отсюда
| ω = | Ω
2 |
, где Ω = | 2 π
Tn |
. |
Приведенный пример показывает, что все способы оценки устойчивости дают одинаковые результаты. Выбор способа зависит от сложности системы, исходного материала и необходимого вида получаемых данных. Для оценки устойчивости с помощью критерия Гурвица в табл. П.3 приведены расчетные соотношения, связывающие условия устойчивости дискретных систем с коэффициентами характеристического уравнения
D*(z) = 0 при n = 1, ... , 4.
Степень устойчивости в дискретных системах, как и в теории непрерывных систем, оценивается по степени удаления корней характеристического уравнения D*(z) = 0 от линии круга единичного радиуса (рис. 2.2). Косвенной оценкой степени устойчивости и здесь служат запасы устойчивости по фазе Δφ(νc) и амплитуде ΔL (см., например, рис. 2.5). Отметим одну особенность, характерную только для дискретных систем. Пусть передаточная функция системы описывается соотношением
| K*yx(z) = | b0 + b1 z-1 + ... +
bm z-m
c0 + c1 z-1 + ... + cn z-n |
= | P*(z)
D*(z) |
. (2.10) |
В отличие от непрерывных систем в дискретных можно (по крайней мере, в принципе) подобрать параметры системы так, чтобы все коэффициенты ci характеристического уравнения D*(z) = 0 кроме с0, равнялись нулю. В этом случае (2.10) примет вид
| K*yx(z) = | P*(z)
c0 |
, (2.11) |
что соответствует нахождению всех корней характеристического уравнения D*(z) = 0 в центре единичного круга. Если выполняется условие (2.11), то говорят, что линейная дискретная система имеет бесконечную степень устойчивости. Ниже будет показано, что в таких системах переходный процесс заканчивается за конечное и минимально возможное число периодов Тn. Здесь же отметим, что для примера 2.1 условие (2.7) выполняется при k = 1, когда коэффициент c1 при z-1 полинома знаменателя передаточной функции (2.5) становится равным нулю.
Как и в теории непрерывных систем, качество дискретных в переходном режиме оценивается прямыми и косвенными показателями, причем первые из них принято отождествлять с показателями переходной характеристики, а вторыми могут служить дискретные аналоги интегральных оценок - суммарные оценки.
Переходная характеристика замкнутой системы hyx(iTn) определяется как реакция этой системы на дискретную единичную функцию (рис. 2.6)
| x(iTn) = 1(iTn) или x*(z) = | 1
1 - z-1 |
. |

Рис. 2.6. Структурная схема дискретной системы
Она может быть вычислена непосредственно по разностному уравнению
c0hyx(iTn) +
c1hyx[(i-1)Tn] + ... +
cnhyx[(i-n)Tn] =
= b0
1(iTn) + ... + bm 1[(i-m)Tn]
(2.12)
при нулевых начальных условиях или с помощью любого из приемов определения обратного z-преобразования от изображения
| H*yx(z) = x*(z) K*yx(z) = | K*yx(z)
1 - z-1 |
. (2.13) |
Пример 2.2.
Вычислим для условий примера 2.1 переходную характеристику, воспользовавшись двумя указанными способами.
1. Разностное уравнение в z-изображениях для переходной характеристики записывается из выражения (2.6)
H*yx(z) - (1 - k) z-1 H*yx(z) = k z-1 x*(z)
или в оригиналах при x(iTn) = 1(iTn)
hyx(iTn) = k 1[(i - 1)Tn] + (1 - k) hyx[(i - 1)Tn]. (2.14)
Вычисленные с помощью формулы (2.14) переходные характеристики hyx(iTn) для различных коэффициентов преобразования системы k представлены на рис. 2.7. При решении уравнения (2.14) учтено, что 1(iTn) = 0 при i < 0.
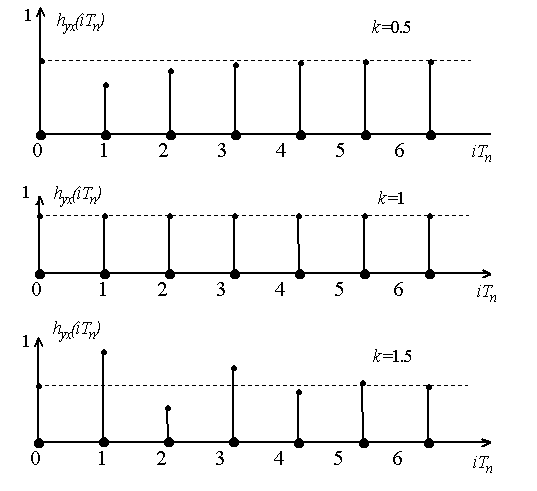
Рис. 2.7. Переходные характеристики дискретной системы при К=0.5 (а); К=1 (б); К=1.5 (в)
2. z-изображение переходной характеристики согласно формулам (2.13) и (2.5) равно
| H*yx(z) = | k z-1
(1 - z-1)[1 - (1 - k) z-1] |
. (2.15) |
С другой стороны, по определению
| H*yx(z) = | ∞ Σ i = 0 |
hyx(iTn) z-1 |
и, следовательно, можно записать
k z-1 = (1 - z-1)[1 - (1 - k)z-1][hyx(0) + hyx(Tn) z-1 + hyx(2Tn) z-2 + ...].
Сравнивая коэффициенты при одинаковых степенях z в левой и правой частях равенства, нетрудно получить значения hyx(iTn), совпадающие с результатом решения уравнения (2.15).
В подразделе 2.1 отмечалось, что при выполнении условий бесконечной степени устойчивости переходный процесс в системе заканчивается за конечное, вполне определенное число периодов Tn. Покажем, что это выполняется и для переходной характеристики, учитывая, что указанные условия имеют место, если все коэффициенты характеристического уравнения замкнутой системы D*(z) = 0 кроме c0, равны нулю, то есть передаточная функция соответствует выражению (2.11). В этом случае согласно (2.13)
| H*yx(z) = | 1
1 - z-1 |
b0 + b1z-1 + ... +
bmz-m
c0 |
или
f0 + f1z-1 + ... + fmz-m = (1 - z-1)[hyx(0) + hyx(Tn) z-1 + hyx(2Tn) z-2 + ...],
где принято обозначение
| fk = | bk
c0 |
Сравнивая теперь коэффициенты при одинаковых степенях z, можно получить
f0 = hyx(0); f1 =
hyx(Tn) - hyx(0);
f2 =
hyx(2Tn) - hyx(Tn); ... ;
fm = hyx(mTn) - hyx[(m -
1)Tn];
0 = hyx[(m + 1)Tn] -
hyx(mTn) или hyx[(m + 1)Tn] =
hyx(mTn).
Таким образом, при бесконечной степени устойчивости переходная характеристика принимает установившееся значение за конечное число периодов m (рис. 2.8), количественно равное порядку полинома числителя передаточной функции системы. Так, в рассмотренном примере, условие бесконечной степени устойчивости k = 1 [см. формулу (2.5)], при этом согласно выражению (2.15)
| H*yx(z) = | z-1
1 - z-1 |
и переходная характеристика принимает установившееся значение за один период.

Рис. 2.8. Переходная характеристика при бесконечной степени устойчивости
Косвенными оценками, учитывающими как длительность, так и форму процесса в переходном режиме, могут служить суммарные оценки. Наиболее общей из них является квадратичная суммарная оценка - аналог интегральной квадратичной оценки в теории непрерывных систем:
| Q* = | ∞ Σ i = 0 |
[e(iTn) - eуст(iTn)]2 = | ∞ Σ i = 0 |
e2пер (iTn)]; (2.16) |
e(iTn) = x(iTn) - y(iTn),
где e(iTn) - ошибка, а eуст(iTn) и eпер(iTn) - ее установившаяся и переходная составляющие (рис. 2.9).
Рассмотрим последовательность вычисления суммарной оценки:
1) находится z-изображение ошибки
e*(z) = x*(z) K*ex(z),
где K*ex(z) - передаточная функция ошибки, описываемая для следящих систем формулой (1.32);

Рис. 2.9. Ошибки дискретной системы
2) по выражению (1.20) для конечных значений (подраздел 1.4) определяется установившееся значение ошибки
| eуст = | lim i → ∞ |
e(iTn) = | lim i → ∞ |
(1 - z-1) e*(z) |
и его z-изображение e*уст(z) = Z{eуст};
3) составляется разность e*пер(z) = e*(z) - e*уст(z) и после подстановки в нее
| z = | 1 + w
1 - w |
записывается e*пер(w);
4) с помощью таблиц интеграла Парсеваля определяется квадратичная суммарная оценка
| Q* = 2I [ | e*пер(w)
1 + w |
]. |
Отметим, что при вычислении e*пер(z) знак разности может получиться как положительным, так и отрицательным, что при дальнейших вычислениях не принимается во внимание, так как рассчитывается квадратичная оценка. Отметим также, что в формуле (2.16) вместо ошибки e(iTn) могут быть использованы выходные y(iTn) или какие-либо другие координаты системы, если их установившиеся значения легко вычисляются.
Пример 2.3.
Определить квадратичную суммарную оценку качества переходного режима в системе для условий примера 2.1, полагая, что на вход замкнутой системы (рис. 1.16) подаются:
1) дискретная единичная функция x(iTn) = x0 1(iTn) или
| x*(z) = | x0
1 - z-1 |
; |
2) дискретная линейная функция x(iTn) = x1 iTn или
| x*(z) = | x1Tnz-1
(1 - z-1)2 |
; |
Здесь z-изображения записаны на основании табл. П.2. для огибающих x(t) = x01(t) и x(t) = x1t. В рассматриваемом примере
| K*(z) = | k z-1
1 - z-1 |
= | P*(z)
Q*(z) |
и, следовательно, передаточная функция ошибки
| K*ex(z) = | Q*(z)
D*(z) |
= | 1 - z-1
1 + z-1(k - 1) |
z-изображение ошибки в случае дискретной единичной функции
| e*(z) = | x0
1 - z-1 |
= | 1 - z-1
1 + z-1(k - 1) |
= | x0
1 + z-1(k - 1) |
. |
Установившееся значение ошибки
| eуст = | lim z → 0 |
(1 - z-1) | x0
1 + z-1(k - 1) |
= 0. |
Изображения переходной составляющей ошибки
| e*пер(z) = | x0
1 + z-1(k - 1) |
или e*пер(w) = | x0(1 + w)
w(2 - k) + k |
. |
Отсюда
| e*пер(w)
1 + w |
= | x0
w(2 - k) + k |
= | α0
β1w + β0 |
. |
Табулированный интеграл для l = 1 (табл. П.1) равен
| I1[ | α0
β1w + β0 |
] = | α02
2(2 - k)k |
и квадратичная суммарная оценка
| Q* = 2I1 = | x02
(2 - k)k |
. |
Для случая дискретной линейной функции аналогично получим

В обоих случаях Q* принимает бесконечные значения при k = 0 и k = 2, соответствующим границе устойчивости системы (пример 2.1) и теряет смысл (становится отрицательной) при k < 0 и k > 2, когда система неустойчива. При k = 1 (бесконечная степень устойчивости) квадратичная суммарная оценка в обоих случаях минимальна.
Так как коэффициент k безразмерен, х0 имеет размерность отслеживаемого параметра, а х1 - его скорости, то в обоих рассмотренных случаях размерность Q* равна квадрату размерности входного процесса. Отметим, что в непрерывных системах квадратичная интегральная оценка качества переходного процесса имеет размерность квадрата размерности входного процесса, умноженного на секунду.
После окончания переходных процессов в системе наступает установившийся режим, качество которого в основном зависит от точности отработки задающих воздействий и степени фильтрации помех. В теории дискретных систем удобным способом оценки качества является оценка точности, то есть анализ ошибок управления. Эти ошибки зависят от параметров системы, ее структуры, от характеристик воздействий и в плане математическом определяются вынужденной составляющей решения разностного уравнения
| yв(iTn) = yx(iTn) + | M Σ j = 0 |
yνj(iTn), |
где yx(iTn) и yν(iTn) - выходные координаты, определяемые соответственно задающим и возмущающим воздействиями, и принято, что на линейную систему поступает М помех.
Для следящих систем ошибка управления представляет собой разность
e(iTn) = x(iTn) - yв(iTn),
то есть в установившемся режиме она равна
| e(iTn) = ex(iTn) + | M Σ j = 0 |
yνj(iTn), (2.17) |
где yx(iTn) = x(iTn) - yx(iTn)- ошибка отработки задающего воздействия (динамическая ошибка) и eν(iTn) = - yν(iTn)- ошибка от возмущающего воздействия (флюктуационная ошибка, если νi(iTn) - случайные процессы).
Оценка качества установившегося режима производится по значению ошибки (2.17) или некоторых функций от нее и имеет особое значение, так как у большинства систем (в том числе у всех следящих) этот режим является основным, определяющим выполнение системой поставленной задачи. Как и в теории непрерывных систем, исследование точности дискретных систем в установившемся режиме производят для регулярных и случайных процессов, описывающих как задающие, так и возмущающие воздействия. Регулярными функциями времени можно аппроксимировать некоторые виды задающих и возмущающих воздействий или их математические ожидания.
Методика расчета ошибок при регулярных воздействиях справедлива (при определенных предпосылках) для процессов любого происхождения, поэтому рассмотрим ее на примере оценки качества дискретной системы при регулярных задающих воздействиях x(iTn), имея в виду и тот факт, что такими воздействиями часто аппроксимируют процессы, соответствующие наиболее тяжелому или наиболее вероятному режимам работы. Будем полагать, таким образом, что известными являются закон изменения x(iTn), структура и параметры дискретной следящей системы (рис. 1.16), то есть ее передаточная функция K*(z).
По отношению к установившемуся режиму дискретные системы, как и непрерывные, делятся на статические и астатические ν-го порядка, где ν = 1, 2, ... для астатических и ν = 0 для статических систем. Ошибки установившегося режима у этих систем определяются как реакция на типовые воздействия вида x(t) = xνtν или x(iTn) = xν(iTn)ν.
Установившееся значение ошибки
| eуст = | lim i → ∞ |
e(iTn) |
может быть найдено по z-изображению e*(z) как
| eуст = | lim z → 1 |
(1 - z-1)e*(z) |
или для рассматриваемой системы (рис. 1.16)
| eуст = | lim z → 1 |
(1 - z-1) K*ex(z) x*(z) = | lim z → 1 |
(1 - z-1) | x*(z)
1 + K*(z) |
(2.18) |
| K*ex(z) = | e*(z)
x*(z) |
, |
где K*ex(z) - передаточная функция ошибки, описываемая формулами (1.32) или (1.37).
Порядок астатизма дискретной следящей системы определяется (см. подраздел 1.8) количеством суммирующих звеньев или, что одно и то же, количеством сомножителей вида (1 - z-1) в передаточной функции разомкнутой системы, которую на основании формулы (1.31) можно представить соотношением

Понятно, что при z = l функция K*ν(z) примет значение, равное коэффициенту преобразования разомкнутой системы
| Kν(z) = kν = |  0 0
 ν ν |
, |
и, следовательно, формулу (2.20) можно записать в виде
| eуст = | lim z → 1 |
(1 - z-1)ν + 1 | x*(z)
(1 - z-1)ν + kν |
, |
позволяющем определять eуст для системы с различным порядком астатизма при воздействиях типа
x(t) = xνtν
При подаче на вход статической системы (ν=0) воздействия х(t) = х0 1(t), где х0 - постоянная величина с размерностью процесса х(t) с z-преобразованием
| x*(z) = | x0
1 - z-1 |
, |
установившаяся ошибка в системе принимает значение
| eуст = | lim z → 1 |
(1 - z-1) | x0
1 - z-1 |
1
1 + k |
= | x0
1 + k |
. |
Если такой же сигнал подать на систему с астатизмом первого порядка (ν = 1), то
| eуст = | lim z → 1 |
(1 - z-1)2 | x0
1 - z-1 |
1
(1 - z-1) + k1 |
= 0. |
При подаче на эту систему воздействия x(t) = x1(t), где x1 - постоянная с размерностью скорости сигнала х(t), имеющего z-изображение
| x*(z) = | Tn z-1
(1 - z-1)2 |
(см.табл.П.2), получим
| eуст = | lim z → 1 |
(1 - z-1)2 | Tn z-1x1
(1 - z-1)2 |
1
(1 - z-1) + k1 |
= | x1 Tn
k1 |
. |
Аналогично можно показать, что при подаче сигналов x(t) = x1(t) и x(t) = x01(t) на систему с астатизмом второго порядка (ν = 2) установившаяся ошибка будет равна нулю. Если воздействие задано в виде
| x(t) = | 1
2 |
x2 t2 или x(iTn) = | 1
2 |
, |
где х2 - постоянная с размерностью ускорения функции х(t), то установившееся значение ошибки
| eуст = | x2Tn2
k2 |
. |
Полученные результаты нетрудно обобщить на системы любого порядка астатизма и убедиться, что при подаче на систему с астатизмом ν-го порядка воздействия вида
| x(t) = | xν tν
ν! |
установившаяся ошибка будет равна
| eуст = | xν Tnν
kν |
. |
Системы астатические ν-го порядка не будут иметь ошибок установившегося режима при подаче на них воздействий вида
| x(t) = | xν1 tν1
ν1! |
, |
если ν1 < ν.
В том случае, когда регулярные воздействия описываются более общими выражениями, для анализа ошибок установившегося режима удобно, как и в непрерывных системах, использовать коэффициенты ошибок. Методика решения задачи заключается в следующем.
Передаточная функция ошибки K*ex(z) (1.32) представляется в виде ряда
| K*ex(z) = |  0 + 0 +  1(1 -
z-1) + ... + 1(1 -
z-1) + ... +  n(1 -
z-1)n n(1 -
z-1)n
 0 + 0 +  1(1 -
z-1) + ... + 1(1 -
z-1) + ... +  n(1 -
z-1)n n(1 -
z-1)n |
= (2.19) |
= D0 + D1(1 - z-1) + D2(1 - z-1)2 + ... ,
который сходится, если z → 1 (i → ∞), то есть если рассматривается установившийся режим. Так как
| K*ex(z) = | e*(z)
x*(z) |
, |
то из выражения (2.19) можно определить изображение ошибки
e*(z) = D0 x*(z) + D1(1 - z-1) x*(z) + D2(1 - z-1)2 x*(z) + ...
и ее оригинал
e(iTn) = D0 x(iTn) + D1Δ1x(iTn) + D2Δ2x(iTn) + ... (2.20)
Здесь учтено, что обратное z - преобразование от изображения вида (1 - z-1)kx*(z) соответствует k-й конечной разности DkΔkx(iTn) (см. п.1.4). Составляющие вида в выражении (2.20) называются ошибками по k-й конечной разности, а коэффициенты Dk - коэффициентами ошибок по соответствующей конечной разности. Ряд ошибки (2.20) сходится, если конечные разности убывают по абсолютной величине с ростом номера их порядка. Практическое применение ряда ошибки имеет смысл, если его составляющие убывают быстро (можно ограничиться лишь несколькими первыми членами), что имеет место при медленных значениях функции х(iTn), то есть когда огибающая является медленно меняющимся воздействием .
Таким образом, предпосылками описываемого метода расчета ошибок являются наличие установившегося режима и узкополосность спектра воздействия, а суть его сводится к вычислению конечных разностей Δkх(iTn) и коэффициентов ошибок Dk. Методика вычисления конечных разностей показана в п.1.4, а коэффициенты Dk, в принципе, могут быть найдены из соотношения (2.19) путем сравнения коэффициентов при одинаковых степенях двучлена 1 - z-1. Для упрощения записи (2.19), а также для согласования форм записи передаточной функции ошибки (1.32) и (1.37) вводят подстановку
χ = 1 - z-1 (2.21)
и тогда формулу (2.19) можно записать следующим образом:
 0 +
0 +  1χ + ... +
1χ + ... +  nχn = (
nχn = ( 0 +
0 +  1χ + ... +
1χ + ... +  nχn)(D0
+ D1χ + D2χ2 + ... ).
(2.22)
nχn)(D0
+ D1χ + D2χ2 + ... ).
(2.22)
Сравнивая в выражении (2.22) коэффициенты при одинаковых степенях χ, нетрудно определить
| D0 = |  0 0
 0 0 |
; D1 = | 1
 0 0 |
( 1 -
D0 1 -
D0 1) 1) |
; D2 = | 1
 0 0 |
( 2 -
D0 2 -
D0 2 -
D1 2 -
D1 1) 1) |
; (2.23) |
| Dk = | 1
 0 0 |
( k - k - |
k Σ j = 1 |
 j j |
Dk - j). |
Пример 2.4.
Структурная схема следящей системы показана на рис. 1.16. Полагая, что
| K(z) = | k z-1
1 - z-1 |
= | P*(z)
Q*(z) |
, |
оценим точность системы в установившемся режиме, если огибающая задающего воздействия х(iTn) аппроксимируется функцией
x(t) = x0 + x1t + 0.5 x2t2. (2.24)
Определим вначале конечные разности дискретного задающего воздействия
x(iTn) = x0 + x1iTn + 0.5 x2(iTn)2.
Согласно методике, изложенной в п. 1.4, получаем

Определим коэффициенты ошибок, для чего запишем
| K*ex(z) = | Q*(z)
D*(z) |
= | 1 - z-1
1 + (k - 1)z-1 |
= | D0 + D1(1 - z-1) + D2(1 - z-1)2 + ... |
Введем подстановку (2.21) и получим
χ = [k + χ(1 - k)](D0 + D1χ + D2χ + ...),
откуда после сравнения коэффициентов при χ0, χ1, χ2, χ3 находим
| D0 = 0; D1 = | 1
k |
; D2 = - | 1 - k
k2 |
; D3 = | (1 - k)2
k3 |
. |
Этот же результат можно получить и по формуле (2.23) для
 0 = 0;
0 = 0;
 1 = 1;
1 = 1;  0 = k;
0 = k;  1 = 1 - k.
1 = 1 - k.
Ряд ошибки (2.20) для рассматриваемого примера запишется в виде
| e(iTn) = | 1
k |
[x1Tn + x2(i - 0.5)Tn2] - | 1 - k
k |
x2Tn2 = |
| Tn
k |
x1 + | Tn
k |
x2[(i - 0.5)Tn + | k - 1
k |
Tn]. |
Установившаяся ошибка нарастает со временем за счет ускорения сигнала (2.24), не компенсируемого системой с одним дискретным интегратором. Это нарастание тем интенсивнее, чем больше период Tn и ускорение x2 и чем меньше коэффициент преобразования, который по условиям устойчивости (см. пример 2.1) меняется в пределах 0 < k < 2. Если ускорение x2 = 0, то
| e(iTn) = eуст = | Tn
k |
x1. |
Этот результат для систем с астатизмом первого порядка получен в начале подраздела.
В предыдущем подразделе предполагалось, что воздействия, поступающие на систему, являются регулярными функциями времени и, следовательно, ошибка управления e(iTn), определяемая соотношением (2.17), тоже имеет регулярный характер. На практике подавляющее большинство возмущающих и задающих воздействий являются случайными, и поэтому ошибка e(iTn) - случайная функция дискретного времени iTn, которую можно представить суммой математического ожидания и центрированной случайной составляющей, то есть
e(iTn) = <e(iTn)> + e0(iTn).
Математическое ожидание <e(iTn)> представляет собой регулярную функцию Времени, методика его определения показана в п.2.3. Случайная составляющая ошибки, как и в непрерывных системах, оценивается по величине ее дисперсии
De(iTn) = <[e0(iTn)]2>.
Рассмотрим методику решения задачи в предположении, что все воздействия представляют собой эргодические стационарные процессы, статистически не зависящие друг от друга. В этом случае дисперсия ошибки
De(iTn) = De
определяется из (2.19) соотношением
| De = Dex + | M Σ j = 0 |
Deνj, |
где Dex и Deν - соответственно дисперсия динамической и флюктуационной ошибок. Так как методика вычисления составляющих дисперсии одинаковая, то рассмотрим ее на примере нахождения дисперсии ошибки отработки задающего воздействия.
Определение величины дисперсии дискретного процесса производится (как и в случае непрерывных систем) по его корреляционной функции, которая для стационарных процессов определяется как
Rex(kTn) = <ex0(iTn) ex0(iTn + kTn)>,
или по спектральной плотности - z-преобразованию от корреляционной функции
| S*ex(z) = | ∞ Σ k = -∞ |
Rex(kTn) z-k. |
Обратное z-преобразование от спектральной плотности определяет корреляционную функцию и поэтому
| Dex = Rex(0) = | 1
2 π j |
 |z|=1 |
S*ex(z) z-1 dz. (2.25) |
Для вычисления дисперсии ошибки надо знать, следовательно, статистические характеристики Rex(kTn) или S*ex(z), которые зависят от статистических характеристик задающего воздействия Rx(kTn) и S*x(z), структуры и параметров системы. Отметим, что корреляционная функция Rx(kTn) и спектральная плотность S*x(z) дискретного процесса x(iTn) несут ту же информацию о случайном процессе, что и в теории непрерывных систем. Корреляционная функция Rx(kTn) представляет собой дискретную функцию своей огибающей Rx(τ) ( рис. 2.10, а), то есть может быть получена из последней подстановкой
τ = kTn,
где k - целые числа.

Рис. 2.10. Корреляционная функция дискретного случайного процесса (а) и дискретного белого шума (б)
При исследовании систем важную роль играют случайные величины с некоррелированными значениями - белый шум. Дискретный белый шум определяется корреляционной функцией (рис. 2.10,б)
| Rx (kTn) = | { | Dx при k = 0 |
| 0 при k ≠ 0 | ||
где Dx - дисперсия процесса, совпадающая по значению с интенсивностью Nx непрерывного белого шума, являющегося образующей дискретного. Спектральная плотность дискретного белого шума не зависит от частоты и равна постоянной величине Nx.
Спектральную плотность ошибки по задающему воздействию S*ex(z) можно представить произведением
S*ex(z) = K*ex(z-1) K*ex(z) Sx(z). (2. 26)
По аналогии с теорией непрерывных систем
S*x(z) = F*x(z) F*x(-1), (2. 27)
где F*x(z) - передаточная функция формирующего фильтра. Тогда формула (2.25) для вычисления дисперсии ошибки с учетом соотношений (2.26) и (2.27) принимает вид
| Dex = | 1
2 π j |
 |z|=1 |
F*x(z) K*ex(z) F*x(z-1) K*ex(z-1) z-1 dz. (2.28) |
При вычислении дисперсии (2.28) удобно пользоваться дискретным аналогом теоремы Парсеваля , согласно которому
| Dex = | 1
2 π j |
j∞ ∫ -j∞ |
F*x(ω)
K*ex(ω)
1 + ω |
. | F*x(-ω)
K*ex(-ω)
1 - ω |
dω. (2.29) |
Таким образом, дисперсия ошибки отработки задающего воздействия в дискретной системе равна удвоенному значению табулированного интеграла:
| Dex = 2I [ | F*x(ω)
K*ex(ω)
1 + ω |
], (2.30) |
где, как и раньше, w - преобразование определяется формулами (2.2).
Дисперсия ошибки, обусловленной возмущающим воздействием ν(iTn) вычисляется аналогично:
| Dex = 2I [ | F*ν(ω)
K*eν(ω)
1 + ω |
], (2.31) |
где F*ν(ω) определяется разложением спектральной плотности помехи S*ν(z) на сопряженные сомножители F*ν(z) F*ν(z-1) с последующей подстановкой
| z = | 1 + ω
1 - ω |
, |
a K*eν(ω) - билинейное преобразование передаточной функции ошибки системы по возмущающему воздействию, совпадающее с точностью до знака с функцией K*yν(ω).
Отметим, что в формулах (2.30) и (2.31) в знаменателе аргумента можно использовать 1 - ω вместо 1 + ω, если это упрощает выкладки. Равноценность замены следует из формулы (2.29).
Пример 2.5.
Структурная схема следящей системы изображена на рис. 1.16. Полагая, что помеха приложена ко входу системы, то есть K*ν(z) = K*(z) вычислим дисперсию флюктуационной ошибки, если
| K*(z) = | k z-1
1 - z-1 |
, |
а помеха - дискретный белый шум с корреляционной функцией
Rν(kTn) = Nνδ(kTn) и спектральной
плотностью S*ν(z) = Nν. Воспользуемся формулой
(2.33). Представим S*ν(z) = 
 откуда
F*ν(w) =
откуда
F*ν(w) =  . Найдем
K*eν(z) из рис. 1.15. Так как помеха приложена ко входу,
то
. Найдем
K*eν(z) из рис. 1.15. Так как помеха приложена ко входу,
то
| K*eν(z) = -K*yx(z) = - | P*(z)
D*(z) |
= - | k z-1
1 + z-1(k - 1) |
. |
Отсюда при
| z-1 = | 1 - ω
1 + ω |
| K*eν = - | k(1 -ω)
ω(2 - k) + k |
, а | F*ν(ω)
K*eν(ω)
1 - ω |
= - | k
k + ω(2 - k) |
. |
Дисперсия ошибки согласно табл. П.3
| Deν = 2I [ |  k k
k + ω(2 - k) |
] = 2 | α20
2 β0β1 |
= | Nνk
2 - k |
. |
По условиям устойчивости (см. пример 2.1) в этой системе 0 < k < 2. В этих пределах дисперсия ошибки растет с увеличением коэффициента k, что объясняется расширением полосы пропускания системы.